Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Найдем числовое значение R в СИ, для чего учтем, что, как следует из закона Авогадро, один моль любого газа при одинаковом давлении и одинаковой температуре занимает один и тот же объем. В частности при Т0 = 273K и давлении Р0 = 105 Па объем одного моля газа равен V0 = 22,4·10–³ м³. Тогда R =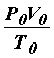= 8,31 Дж/(моль· К).

Уравнение (28) для одного моля газа можно записать в виде

. (29)

Из уравнения (29) легко получить уравнение для любой массы газа. Газ массой m займет объем V = V0(m/M), где М – масса 1 моль, m/M – число молей газа. Умножив обе части уравнения (29) на m/M, получим .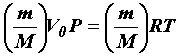

Так как 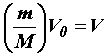, то окончательно получаем

. (30)

Уравнение (30) называется уравнением Менделеева – Клапейрона и является основным уравнением, связывающим параметры газа в состоянии теплового равновесия. Поэтому его называют уравнением состояния идеального газа.

Температура - мера средней кинетической энергии

Сравнивая уравнение состояния идеального газа и основное уравнение кинетической теории газов, записанные для одного моля (для этого число молекул N возьмём равным числу Авогадро NА), найдём среднюю кинетическую энергию одной молекулы:

и .

Откуда

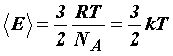. (31)

Средняя кинетическая энергия поступательного движения молекулы не зависит от её природы и пропорциональна абсолютной температуре газа T. Отсюда следует, что абсолютная температура является мерой средней кинетической энергии молекул.

Величина R/NА = k в уравнении (31) получила название постоянной Больцмана и представляет собой газовую постоянную, отнесенную к одной молекуле:

k = 1,38·10-23 Дж/К-23.

Так как 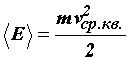=kТ, то средняя квадратичная скорость равна

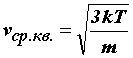. (32)

Подставляя значение средней кинетической энергии поступательного движения молекул (31) в основное уравнение молекулярно–кинетической теории газов, получим другую форму уравнения состояния идеального газа:

P = n0kT. (33)

Давление газа пропорционально произведению числа молекул в единице объема на его термодинамическую температуру.

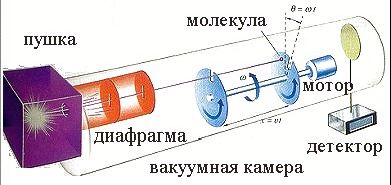
На рис. приведена схема опыта Штерна для определения скорости молекул газа.

В нагревателе с поверхности проволоки, раскаленной электрическим током, испаряются атомы серебра. Попадая из нагревателя через отверстие в вакуумную камеру, молекулы пара с помощью системы щелей формируются в узкий пучок, направленный в сторону двух дисков, вращающихся с угловой скоростью  .Диски используются для сортировки молекул по скоростям. Угол между прорезями в дисках . Расстояние между дисками X в процессе эксперимента не изменяется. Для того, чтобы молекула пара попала на приемник детектора частиц, она должна пройти через прорези в дисках. Для этого время прохождения молекулы, движущейся со скоростью V между дисками, должно быть равно времени поворота прорези второго диска на угол .

Поэтому

V=· X/ 

Рекомендуем скачать другие рефераты по теме: методы курсовой работы, шарарам ответы.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата