Предыдущая страница реферата | 1  2  3  4  5  6

Положим, что в формуле (1). Тогда , , …, , ; при x=b все функции v, v’, …,  обращаются в нуль. Пользуясь для u, u’, u’’, … функциональным обозначением f(x), f’(x), f’’(x), …, перепишем (1) в виде

.

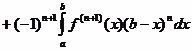Отсюда получается формула Тейлора с дополнительным членом в виде определенного интеграла

.

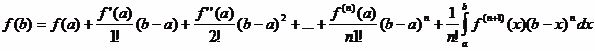Заменим здесь b через x, а  через :

.

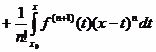Новое выражение для дополнительного члена, не содержит никаких неизвестных чисел.

Если угодно, из этого выражения можно было бы вывести и уже знакомые нам формы дополнительного члена. Например, воспользовавшись тем, что множитель  подинтегральной функции не меняет знака, можно применить к последнему интегралу обобщенную теорему о среднем

,

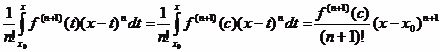где с содержится в промежутке . Таким образом, мы вновь получили лангранжеву форму дополнительного члена.

5. Заключение.

В курсовой работе даны определения определенного и несобственного интеграла и его виды, рассмотрены вопросы некоторого приложения определенного интеграла. В частности, формула Валлиса, имеющая историческое значение, как первое представление числа p в виде предела легко вычисляемой рациональной варианты, а также вычисление интеграла Эйлера-Пуассона с помощью этой формулы. Рассмотрен способ получения формулы Тейлора с дополнительным членом в интегральной форме.

Формулой Валлиса в теоретических исследованиях пользуются и сейчас (например, при выведении формулы Стирлинга). Что касается фактического приближенного вычисления p, то существуют методы, гораздо более быстро ведущие к цели.

Интеграл Эйлера-Пуассона применяется при вычислении более сложных несобственных интегралов, встречается в теории вероятности.

Новое выражение для дополнительного члена в формуле Тейлора интересно тем, что оно не содержит никаких неизвестных чисел.

Данную курсовую работу можно использовать в качестве лекционного и справочного материала.

Список литературы

Фихтенгольц Г. М. «Курс дифференциального и интегрального исчисления»(II том) – Москва, 1970г.

Пискунов Н.С. «Дифференциальное и интегральное исчисления»(I том) - Москва, 1970г.

Эрмит Ш. «Курс анализа» - Москва, 1936г.

Скачали данный реферат: Javlenskij, Великий, Унгерн, Сиянкин, Balashov, Peskov.
Последние просмотренные рефераты на тему: ценные бумаги реферат, решебник 5 класс, древния греция реферат, реферат по биологии 7 класс.





Предыдущая страница реферата | 1  2  3  4  5  6