Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

А потому нетрудно понять наших современников, японцев С.Иномату и М.Кумаду, которые попытались придать процессу спуска по антиградиенту вышеописанный физический смысл. Между прочим, их метод так и назвали «методом тяжёлого шарика». Только разумеется, при его использовании не катают глобус по макету функции, а лишь решают дифференциальные уравнения движения.

Немало трудностей ждёт того, кто ищет экстремум функции, но одна из самых коварных – это овраги. Любой из методов, даже наиболее совершенный в вычислительном отношении метод наискорейшего спуска Л.В.Канторовича, известного советского математика, приводит к беспомощному метанию по дну оврага. Поэтому советские математики И.М.Гельфанд и М.Л.Цетлин и предложили «овражный поиск», который позволяет выследить дно оврага. Итак, как мы видим, почти все численные методы поиска наилучшего направления спуска так или иначе связаны с антиградиентом. Правда, оказалось, что труды по отысканию антиградиента не всегда вознаграждаются качеством найденного направления спуска, и советский учёный Л.А.Растригин предложил вообще не тратить сил и машинного времени на поиск антиградиента, а шагать куда себе вздумается, то бишь по случайному направлению. И представьте, результаты такого образа действий оказались ничуть не хуже в вычислительном отношении, чем поиски наилучших путей. Иначе говоря, не настолько эти наилучшие пути превосходят по качеству случайный, чтобы стоило тратить время на их поиск. Разумеется, чтобы выбрать направление спуска случайным образом, не крутятся на месте с закрытыми глазами – для этого в машине используют датчики случайных чисел. И вообще численную сторону методов нелинейного программирования трудно продемонстрировать на бумаге – это существенно машинные методы.

Но вернёмся к потерпевшим кораблекрушение и узнаем, кому из них сопутствовал успех в поиске воды.

Там, за перевалом

Итак, все разбрелись в поисках воды, кроме кучки Скептиков.

– Дьявольская жажда! – промолвил один из них. – Неужели вас она не мучит?

– Не меньше, чем вас, – ответил Винер от имени остальных. – И я охотно двинулся бы на поиски воды, если бы меня убедил какой-то из предложенных способов. Но увы! Если мы начнём таким способом искать высшую точку Земли, то вместо Эвереста окажемся на вершине соседнего холмика. И самое ужасное то, что у нас нет никакого средства отличить этот холмик от Эвереста. Если, конечно, не привлечь на помощь математике обыкновенную географию.

– Как это нет? Почему? – поинтересовался молодой Скептик, которого скептицизм не отучил ещё задавать вопросы.

– Очень просто. С помощью фонарика мы способны лишь убедиться, что из данной точки пути ведут вниз. А что там, дальше? Вот тут наши друзья предложили ряд способов, – он снисходительно показал на оставшиеся листки из судового журнала. – Они исходили из того, что на острове только одна низина. А если их много, и вода лишь в самой низкой из этих низин (рис. 5)? Спуск приведёт нас в точку A, а вода в точке B – там гуще горизонтали и, следовательно, ниже отметка. Задумайтесь над этим.

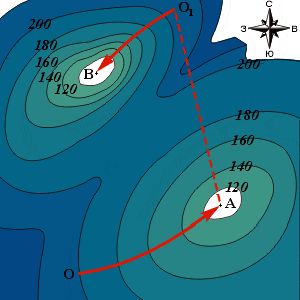
Рис. 5

– Я уже задумывался, – сказал первый Скептик. – И решил действовать так. Сначала пойду куда глаза глядят. Потом спущусь в ближайшую низину и замерю её высоту высотомером. Запомню её расположение и перейду в новую случайную точку. Из нее снова спущусь в низину и снова взгляну на высотомер. Допустим, он покажет на сей раз меньшую высоту. Это значит, что вторая низина ниже первой, и там больше шансов найти воду. Затем...

– Что будет затем, ясно, – прервали его. – Но уверены ли вы, что найдёте воду прежде, чем свалитесь с ног?

– Могу ли я быть в этом уверен? Ведь я же Скептик! Просто это лучше, чем стоять сложа руки.

И первый Скептик скрылся в темноте.

Второй Скептик привязывал в это время шпагат к футбольному мячу, невесть как оказавшемуся среди приборов.

– Уж не собираетесь ли вы по следам Кумады? – спросил его Винер, одновременно к чему-то прислушиваясь.

– Вы почти угадали. Но я поступлю несколько иначе. Спустившись в низину, я замерю её высоту, а затем буду бить по мячу ногой в разные стороны. Если мяч будет каждый раз скатываться назад, значит, поблизости нет перевала, за которым новая низина. Если же мяч не скатится ко мне, я отправлюсь по шпагату за ним, приду в низину, в которой он застрял, и замерю её высоту. И так далее...

– Но так можно обнаружить лишь недалёкий перевал.

– Что вы! У меня сильный удар. Меня обычно просят ударить от ворот.

– В таком случае может произойти ещё худшее: вы перебьёте мяч через низину, которую ищите. Мяч не вернётся к вам, но уведёт вас от цели.

– Вы правы... Тогда, пожалуй, я не буду стараться каждый раз ударить посильнее. Я буду чередовать сильные и слабые удары. Или, скажем, буду постепенно усиливать их, начав со слабых.

– Что ж, я желаю вам успеха. Если наградой вам и не послужит вода, то во всяком случае вы повысите свою спортивную форму.

– А я поступлю иначе, – обратился третий Скептик к Винеру. – Я отправлюсь просто бродить по острову, не стараясь найти наилучшее направление, и буду поглядывать на высотомер. Побродив, замечу, где самая низкая точка, и уже там начну поиски воды. Все эти разговоры убедили меня, что если у нас нет карты острова, то никакой разумной стратегии движения быть не может. Так зачем же тогда тратить время на возню с приборами? Но вы, кажется, не слушаете меня?

Где кончается асфальт

Рекомендуем скачать другие рефераты по теме: пример курсовой работы, реферат на тему предприятие.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата