Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Программное обеспечение является одной из частей кардиографической системы. Данный раздел включает в себя три основных этапа: фильтрация сигналов, анализ данных и постановка диагноза на основе этих характеристик.

Данная работа посвящена изучению вопроса идентификации особенностей ЭКГ, как одного из шагов комплексного анализа сигнала. Это весьма важный этап так как допущение ошибки здесь сильно сказывается на врачебном заключении.

2. ПОСТАНОВКА ЗАДАЧИ

В рамках задачи предобработки и вычислении параметров ЭКГ в компьютерном кардиологическом комплексе, необходимо разработать модуль анализа основных характеристик электрокардиограммы человека на базе алгоритма непрерывного вейвлет-преобразования.

Для этого следует:

изучить форму, стандарты описания и обозначения ЭКГ; построить модель идеальной ЭКГ провести сравнительный анализ эффективности системы Matlab и разработанного модуля проанализировать временные затраты с учетом параметров съема ЭКГ и аппаратного обеспечения

При проведении исследований использовать систему Matlab 5.0, для разработки модуля использовать среду программирования Delphi 5.0.

3. ПОДХОДЫ К АНАЛИЗУ НЕСТАЦИОНАРНЫХ СИГНАЛОВ 3.1. Методы обработки нестационарных сигналов

Большинство медицинских сигналов имеет сложные частотно-временные характеристики. Как правило, такие сигналы состоят из близких по времени, короткоживущих высокочастотных компонент и долговременных, близких по частоте низкочастотных компонент.

Для анализа таких сигналов нужен метод, способный обеспечить хорошее разрешение и по частоте, и по времени. Первое требуется для локализации низкочастотных составляющих, второе – для разрешения компонент высокой частоты.

Вейвлет преобразование стремительно завоевывает популярность в столь разных областях, как телекоммуникации, компьютерная графика, биология, астрофизика и медицина. Благодаря хорошей приспособленности к анализу нестационарных сигналов оно стало мощной альтернативой преобразованию Фурье в ряде медицинских приложений. Так как многие медицинские сигналы нестационарны, методы вейвлет анализа используются для распознавания и обнаружения ключевых диагностических признаков.

Преобразование Фурье представляет сигнал, заданный во временной области, в виде разложения по ортогональным базисным функциям (синусам и косинусам), выделяя таким образом частотные компоненты. Недостаток преобразования Фурье заключается в том, что частотные компоненты не могут быть локализованы во времени, что накладывает ограничения на применимость данного метода к ряду задач (например, в случае изучения динамики изменения частотных параметров сигнала на временном интервале).

Существует два подхода к анализу нестационарных сигналов такого типа. Первый – локальное преобразование Фурье (short-time Fourier transform). Следуя по этому пути, мы работаем с нестационарным сигналом, как со стационарным, предварительно разбив его на сегменты (окна), статистика которых не меняется со временем. Второй подход – вейвлет преобразование. В этом случае нестационарный сигнал анализируется путем разложения по базисным функциям, полученным из некоторого прототипа путем сжатий, растяжений и сдвигов. Функция прототип называется материнским, или анализирующим вейвлетом.

3.2 Краткий обзор преобразования Фурье

Классическим методом частотного анализа сигналов является преобразование Фурье, суть которого можно выразить формулой (1)

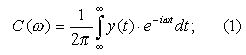
Результат преобразования Фурье – амплитудно-частотный спектр, по которому можно определить присутствие некоторой частоты в исследуемом сигнале.

В случае, когда не встает вопрос о локализации временного положения частот, метод Фурье дает хорошие результаты. Но при необходимости определить временной интервал присутствия частоты приходится применять другие методы.

Одним из таких методов является обобщенный метод Фурье (локальное преобразование Фурье). Этот метод состоит из следующих этапов:

1. в исследуемой функции создается “окно” – временной интервал, для которого функция f(x)¹ 0, и f(x)=0 для остальных значений;

2. для этого “окна” вычисляется преобразование Фурье

3. “ окно” сдвигается, и для него также вычисляется преобразование Фурье

“Пройдя” таким “окном” вдоль всего сигнала, получается некоторая трехмерная функция, зависящая от положения “окна” и частоты.

Данный подход позволяет определить факт присутствия в сигнале любой частоты, и интервал ее присутствия. Это значительно расширяет возможности метода по сравнению с классическим преобразованием Фурье, но существуют и определенные недостатки. Согласно следствиям принципа неопределенности Гейзенберга в данном случае нельзя утверждать факт наличия частоты w 0 в сигнале в момент времени t0 - можно лишь определить, что спектр частот (w 1,w 2) присутствует в интервале (t1,t2). Причем разрешение по частоте (по времени) остается постоянным вне зависимости от области частот (времен), в которых производится исследование. Поэтому, если, например, в сигнале существенна только высокочастотная составляющая, то увеличить разрешение можно только изменив параметры метода. В качестве метода, не обладающего подобного рода недостатками, был предложен аппарат вейвлет анализа. [2]

3.3 Основные положения вейвлет-анализа

Различают дискретный и непрерывный вейвлет анализ, аппарат которых можно применять как для непрерывных, так и для дискретных сигналов.

Cигнал анализируется путем разложения по базисным функциям, полученным из некоторого прототипа путем сжатий, растяжений и сдвигов (2). Функция-прототип называется анализирующим (материнским) вейвлетом.

Вейвлет - функция должна удовлетворять 2-м условиям:

1. Среднее значение (интеграл по всей прямой) равен 0.

2. Функция быстро убывает при t ® ∞.

Обычно, функция-вейвлет обозначается буквой ψ.

Рекомендуем скачать другие рефераты по теме: контрольные работы 8 класс, реферат на тему современные.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата