Независимость событий в примере Бернштейна с правильным тетраэдром

Реферат по дисциплине: «Теория вероятности и математическая статистика»

Выполнил: Апаз С.В.

Крымский Экономический Институт Киевского Национального Экономического Университета

Симферополь — 2002

Независимость событий

Понятие независимости является одним из важнейших понятий теории вероятностей.

События А и В называются независимыми, если

Р(АВ) = Р(А)Р(В).                  (1.1)

В случае Р(А) = 0 и Р(В) > 0 эквивалентны любому из равенств

Р(А|В) = Р(А), Р(В|А) = Р(В).              (1.2)

Определение независимости в форме (1.1) симметрично относительно А и В; условие (1.1) несколько шире, чем условия (1.2).

Если математическая модель, описывающая некоторые опыт, подобрана достаточно хорошо, то независимым события реального опыта соответствуют событиям модели, независимые в смысле определения (1.1). Пусть, например, опыт заключается в том, что один раз бросают две симметричные монеты. В обозначениях положим Ω = {ГГ, РР, РГ, ГР}; А = {ГГ, ГР} – первая монета выпала гербом вверх, В = {РГ, Г} – вторая монета выпала гербов вверх. Предполагая равновероятность элементарных событий, получим

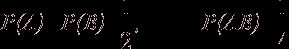
Таким образом, Р(АВ) = Р(А)Р(В). события А и В оказались независимыми в смысле определения (1.1).

Условная вероятность. Независимость событий и испытаний.

Начнем с примеров. Пусть эксперимент состоит в троекратно подбрасывании симметричной монеты. Вероятность того, что герб выпадет ровно один раз, т.е. что произойдет одно из элементарных событий (грр), (ргр), (ррг), в классической схеме равно 3/8. обозначим это событие буков А. Предположим теперь, что об исход эксперимента дополнительно известно, что произошло событие

В = {число выпавших гербов нечетно}

Какова вероятность события А при этой дополнительной информации? Событие В состоит из 4 элементарных исходов. Событие же А составляется из 3 исходов события В. в рамках классической схемы естественно принять новую вероятность события А равной ¾.

Рассмотрим еще один более общий пример. Пусть задана классическая схема с n исходами. Событие А состоит из r исходов, событие В из m исходов, а событие АВ содержит k исходов. Вероятность события А при условии, что произошло событие В, по аналогии с предыдущим примером, естественно определить следующим образом:

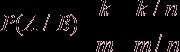
Полученное отношение равно 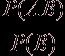, так как

Р(АВ) = k/n

Р(В) = m/n.

Мы можем перейти теперь ко общему определению.

Пусть задано вероятностное пространство áΩ, ξ, Рñ и пусть А и В – произвольны события. Если Р(В) > 0, то условная вероятность события А при условии , что произошло событие В, по определению полагается равной

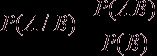
Рекомендуем скачать другие рефераты по теме: решебник 6, евгений сочинение.





1  2  3 | Следующая страница реферата