Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

 Обозначим: E(Р) тождественную машину, т.е. Е(Р)=Р

СOPY(Р) копирующую машину, т.е. СOPY(Р)=Р||Р,

где ||ÏS.

BRANCH(P) - эта машина переходит либо в состояние р1, либо в состоянии ро. Ее программа состоит из 4-х команд:

1qo®1р1П

||р1®||р1П

0qo®0роП

||ро®||роП

Построим машину

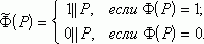
Эта машина строится по следующей формуле:

Согласно теоремам 3.1 и 3.2., мы можем построить машину , зная Е, Ф и COPY. Теперь, имея , BRNCH, A и В, можно построить машину С следующим образом:

Машина  o BRANCH  заканчивает свою работу либо в состоянии р1, если слово P обладает нужным свойством, либо в состоянии ро, находясь в начале  слова P. Поэтому, если принять у машины А состояние р1, как начальное, а у машины В состояние ро, как начальное, то машина А будет включена при условии, что Ф(Р)=1, а машина В будет включена, если Ф(Р)=0.

 Правило композиции, определяемое этой теоремой будем записывать, если Ф то А иначе В.

Теорема 3.4.  Для любых машин А и Ф можно эффективно построить машину L такую, что

L(P)={ Пока Ф(Р)=1, применяй А }

Доказательство: Заменим в доказательстве теоремы 3.3. машину В машиной Е, а заключительное состояние в машине В заменим на начальное состояние в машине  . В итоге получим нужный результат.

Теорема 3.5.  (Бомм, Джакопини, 1962)

Любая Машина Тьюринга может быть построена с помощью операции композиций o, || , если Ф, то А иначе В, пока Ф применяй А.

Эту теорему мы даем здесь без доказательства.

Следствие 3.1.  В силу Тезиса Тьюринга, любая интуитивно вычислимая функция может быть запрограммирована в терминах этих операций.

Следствие 3.2  Мы получили что-то вроде языка, на котором можно описывать новую Машину Тьюринга, используя описания уже существующих, а затем, используя теоремы 3.1 - 3.4, построить её функциональную схему.

Следствие 3.3  Алгоритм - это конструктивный объект. В случае Машины Тьюринга атомарными объектами являются команды, а теорема 3.5 определяет правила композиции.

Выводы:

Рекомендуем скачать другие рефераты по теме: контрольные работы 9 класс, доклады бесплатно.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата