О вычислении коэффициентов и узлов одной  квадратурной формулы

Асп. Плиева Л.Ю.

Кафедра математического анализа.

Северо-Осетинский государственный университет

Статья посвящена одному квадратурному процессу, построенному Д.Г. Саникидзе в 1965 г. для вычисления некоторых несобственных интегралов. Вычислены коэффициенты, узлы для конкретных значений .

В приближенных вычислениях особое место занимают квадратурные формулы с наивысшей степенью точности. Их преимущество перед другими обычными квадратурными формулами заключается в том, что в них применяется минимальное количество узлов, коэффициентов и результаты получаются с наименьшей погрешностью. Квадратурные формулы указанного типа были построены еще в XIX в. Гауссом. Поэтому такие квадратурные формулы получили название квадратурных формул Гаусса. В дальнейшем в развитие этой теории значительный вклад внесли А.Крылов и В.Крылов [1].

Здесь же мы рассмотрим квадратурную формулу, которая была построена в 1965 г. грузинским математиком Саникидзе Д.Г. [2]. Он построил ее для вычисления несобственных интегралов вида:

, (1)

где  – весовая функция и , а  – дифференцируемая до определенного порядка функция.

Итак, квадратурная формула для (1) имеет вид:

,

где ,

, ,

,

.

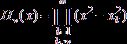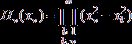Здесь  являются узлами квадратурной формулы, ,  – коэффициентами, а  – остаточным членом.

В статье Д.Г.Саникидзе [2] приведена таблица узлов и коэффициентов для случая , которые не позволяют вычислить интеграл с более высокой степенью точности из-за отсутствия дальнейших значений узлов и коэффициентов.

Наша задача заключалась в том, чтобы построить указанную квадратурную формулу для конкретных значений .

В [2]  вычисляют из следующей системы нелинейных уравнений:

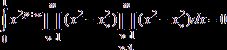 (). (2)

Используя свойства ортогональности многочленов, можно (2) заменить следующей эквивалентной системой:

. (3)

Отсюда для любого  мы будем получать формулы Вьета, т. е. наша задача свелась к решению обыкновенного алгебраического уравнения -ой степени:

 (4)

где . Для его решения и вычисления коэффициентов была составлена программа на языке Паскаль для значений:

 .

Рекомендуем скачать другие рефераты по теме: скачать на телефон шпаргалки, сочинение.





1  2  3 | Следующая страница реферата