Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

            Погрешностями измерений занимается метрология [88].Отметим справедливость следующих фактов:

            а) для большинства реальных измерений невозможно полностью исключить систематическую ошибку:  ;

            б) распределение не всегда является нормальным [94];

            в)  и  обычно нельзя считать независимыми случайными величинами;

            г) распределение погрешностей оценивается по результатам случайных наблюдений, следовательно, полностью известным считать его нельзя; зачастую исследователь располагает лишь границами для систематической погрешности и оценками таких характеристик для случайной погрешности, как дисперсия или размах.

            Приведенные факты показывают ограниченность области применимости модели погрешностей, в которой  и  рассматриваются как независимые случайные величины, причем  имеет нормальное распределение с нулевым математическим ожиданием.

            Строго говоря, результаты наблюдения всегда имеют дискретное распределение, поскольку описываются числами с небольшими (1 - 5) числом значащих цифр. Возникает дилемма: либо признать, что непрерывные распределения - фикция, и прекратить ими пользоваться, либо считать, что непрерывные распределения имеют "реальные" величины , которые мы наблюдаем с принципиально неустранимой погрешностью . Первый выход в настоящее время нецелесообразен, так как потребует отказаться от большей части разработанного математического аппарата. Из второго следует необходимость изучения влияния неустранимых погрешностей на статистические выводы.

            Погрешности  можно учитывать либо с помощью вероятностной модели (- случайная величина, имеющая функцию распределения, вообще говоря, зависящую от ), либо с помощью нечетких множеств. Во втором случае приходим к теории нечетких чисел, развитой П.Б.Шошиным [95] с целью описания поведения человека, и к интервальной статистике [9, 13, 19 - 25, 96 - 101].

            Другой источник появления  связан с принятой в конструкторской и технологической документации системой допусков на контролируемые параметры изделий и деталей, с использованием шаблонов при проверке контроля качества продукции. В этих случаях характеристики  определяются не свойствами средств измерения, а применяемой технологией проектирования и производства. В терминах математической статистики сказанному соответствует группировка данных, при которой мы знаем, какому из заданных интервалов принадлежит наблюдение, но не знаем точного значения результата наблюдения. Применение группировки может дать экономический эффект, поскольку зачастую легче (в среднем) установить, к какому интервалу относится результат наблюдения, чем точно измерить его.

Объекты нечисловой природы как результат статистической обработки данных.

            Объекты нечисловой природы появляются не только на "входе" статистической процедуры, но и в процессе обработки данных, и на "выходе" в качестве итога статистического анализа.

            Рассмотрим простейшую прикладную постановку задачи регрессии. Данные имеют вид . Цель состоит в том, чтобы с достаточной точностью описать как полином от , т.е. модель имеет вид

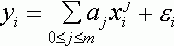 ,                                    (5)

 где  - неизвестная степень полинома;  - неизвестные коэффициенты многочлена; ,  - погрешности, которые для простоты примем независимыми и имеющими одно и то же нормальное распределение. Распространенная процедура такова [102]: сначала пытаются применить модель (5) для линейной функции (  = 1), при неудаче переходят к многочлену второго порядка ( = 2), если снова неудача, то берут модель (5) с = 3 и т.д. (адекватность модели проверяют по F-критерию Фишера).

Обсудим свойства этой процедуры в терминах математической статистики. Если степень полинома задана ( = ), то его коэффициенты оценивают методом наименьших квадратов, свойства этих оценок хорошо известны (см., например, [62, гл.26}). Однако в описанной выше реальной постановке  тоже является неизвестным параметром и подлежит оценке. Таким образом, требуется оценить объект , ., множество значений которого можно обозначить  Это - объект нечисловой природы, обычные методы оценивания его неприменимы, так как  - дискретный параметр. В рассматриваемой постановке методы оценивания носят в основном эвристический характер {103, гл.12}. Свойства  описанной выше распространенной процедуры рассмотрены в работе {104}; в которой показано, что m при этом оценивается несостоятельно (см. также .{14,18}).

            В более общем случае линейной регрессии данные имеют вид , где - вектор предикторов (объясняющих переменных), а модель

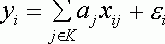                                 (6)

 ( - некоторое подмножество множества ;- те же, что и в модели (5);  - неизвестные коэффициенты при предикторах с номерами из {103]). Модель (5) сводится к модели (6), если

.,

            В модели (5) есть естественный порядок ввода предикторов в рассмотрение - в соответствии с возрастанием степени, а в модели (6) естественного порядка нет, поэтому здесь стоит произвольное подмножество множества предикторов. Есть только частичный порядок - чем мощность подмножества меньше, тем лучше. Модель (6) особенно актуальна в задачах управления качеством продукции, в медицине и социологии, когда из большого числа факторов, предположительно влияющих на изучаемую переменную, надо отобрать по возможности наименьшее число значимых факторов и с их помощью сконструировать прогнозирующую формулу (6).

            Задача оценивания модели (6) разбивается на две последовательные задачи: оценивание множества - подмножества множества всех предикторов, а затем - неизвестных параметров . Методы решения второй задачи хорошо известны и изучены. Гораздо хуже обстоит дело с оцениванием объекта нечисловой природы . Существующие методы  [103] - в основном эвристические, они зачастую не являются даже состоятельными. Понятие состоятельности в данном случае требует определения. Пусть - истинное подмножество предикторов, т.е. подмножество, для которого справедлива модель (6), а подмножество предикторов  - его оценка. Оценка  является состоятельной, если

,

где  - знак симметрической разности множеств;  означает число элементов в множестве , а предел понимается в смысле сходимости по вероятности.

            Задача оценивания в моделях регрессии, таким образом, разбивается на две - оценивание структуры модели и параметров при заданной структуре. в модели (5) структура описывается неотрицательным целым числом , в модели (6) - множеством . Структура - объект нечисловой природы. Задача ее оценивания сложна, в то время как задача оценивания численных параметров при заданной структуре хорошо изучена, разработаны эффективные ( в смысле математической статистики) методы.

Рекомендуем скачать другие рефераты по теме: страница реферата, курсовик.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата