Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

А. Если æ, то  и уравнение (1) имеет вещественные корни различных знаков.

В. Если 0< æ<1, то  и уравнение (1) имеет комплексные корни.

С. Если æ>1, то  и уравнение (1) имеет вещественные корни одного знака.

Соответственно этим случаям Пирсон различает три главных типа своих кривых, которые он назвал соответственно типами I, IV и VI. Затем æ может равняться , что дает переходные типы кривых. Наконец, присоединяя некоторые дополнительные условия, мы можем увеличить число переходных типов. Всего система кривых Пирсона заключает 12 типов и нормальную кривую.

В своих разработках Колмогоров А. Н. и Марков А. А. доказали, что любой закон распределения может быть записан в виде одного из двенадцати типов кривых Пирсона, поэтому для решения задачи идентификации используется метод Пирсона.

§ 2. Основные типы кривых Пирсона.

В этом параграфе будут рассмотрены основные типы кривых распределения вероятностей, предложенные и классифицированные Пирсоном.

Тип I.

 Пусть æ<0. Тогда

 и уравнение (2) имеет вещественные корни различных знаков: , так что можем записать

.

Тогда правая часть уравнения  (1)  может быть представлена в виде:

,

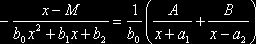где

.

Пусть еще

.

Тогда уравнение (1) перепишется в виде

  и общий интеграл его можно представим в виде

,

где  и значения  и  должны удовлетворять условиям

.

Тип I получается, если  заключается в интервале . Тогда

 и

Рекомендуем скачать другие рефераты по теме: решебник по 5, темы рефератов по физике.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата