Ортогональные полиномы и кривые распределения вероятностей

Карпова Наталия Анатольевна

Санкт-Петербургский государственный университет

Факультет прикладной математики – процессов управления

Кафедра математического моделирования энергетических систем

Санкт Петербург

2002

Введение.

Математическая статистика является наукой, которая изучает соотношения, столь глубоко проникающие в суть вещей, что их можно встретить при самых различных обстоятельствах. Результаты исследований, полученные с помощью аппарата математической статистики, используются в самых различных областях науки и техники, таких как биология, медицина, анатомия, геология, экология, экономика, и т.д.

Данная дипломная работа посвящена рассмотрению двух основных задач математической статистики:

получению кривой распределения вероятностей по имеющейся выборке;

нахождению зависимости между двумя случайными величинами, заданными своими выборками.

Для решения первой задачи используются различные методы. В данной работе рассмотрен метод Карла Пирсона, представителя английской школы статистики. Им было получено дифференциальное уравнение

,

а так же введен критерий æ (каппа Пирсона), с помощью которого Пирсон классифицировал решения этого дифференциального уравнения и представил их в виде двенадцати типов.

Позже в своих теоретических исследованиях Колмогоров А. Н. и Марков А. А. доказали, что любой закон распределения может быть записан в виде одного из двенадцати типов кривых Пирсона, поэтому для решения данной задачи используется метод Пирсона нахождения кривой распределения.

Для решения второй задачи используется метод П.Л. Чебышева, создателя Санкт – Петербургской математической школы. В статистике имя знаменитого русского математика П. Л. Чебышева (1821-1894) известно главным образом по так называемому неравенству Чебышева, которое он предложил для распределения вероятностей, и которое имеет силу для любого статистического распределения численностей.

Однако за последнее время в статистике всё большее значение приобретают ортогональные полиномы Чебышева, которые имеют особое значение при определении множественной и криволинейной регрессии и при вычислении коэффициентов обобщённой функции нормального распределения вероятностей.

Чебышев предложил общую интерполяционную формулу, при которой возможно интерполирование в самых разнообразных случаях. Эта интерполяционная формула удовлетворяет условиям метода наименьших квадратов и выражена при помощи его ортогональных полиномов. Общая интерполяционная формула, или, иначе ряд Чебышева, предложен Чебышевым в 1855 году. Она имеет вид

 .

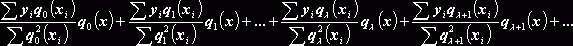Таким образом в дипломной работе рассматриваются два метода:

метод Пирсона нахождения кривых распределения вероятностей,

метод Чебышева получения ортогональных полиномов,

которые были положены в основу обобщенного метода Грамма – Шарлье нахождения кривой распределения вероятностей.

Глава 1. Система кривых Пирсона.

В данной главе ставится задача нахождения закона распределения случайной величины в удобном для практического использования виде. Для ее решения рассматривается подход К. Пирсона, который является выдающимся представителем английской статистической школы.

§ 1. Дифференциальное уравнение Пирсона.

Рассмотрим случайную величину, заданную своей выборкой , таким образом, можем записать  - статистической распределение. Ставится задача нахождения закона распределения случайной величины в удобном для практического использования виде.

Метод Пирсона заключается в том, что мы рассматриваем дифференциальное уравнение Пирсона:

Рекомендуем скачать другие рефераты по теме: первый снег сочинение, реферати українською.





1  2  3 | Следующая страница реферата