Основные определения и теоремы к зачету по функциональному анализу

Определение:  Элемент наилучшего приближения – L – линейное  многообразие, плотное в E. "e "xÎE $u: ║x-u║1-e

Определение:  Полное нормированное пространство- любая фундаментальная последовательность сходиться.

Теорема:  О пополнении нормированного пространства. Любое нормированное пространство можно считать линейным многообразием, плотным в некотором полном нормированном пространстве.

Определение:  Гильбертово пространство – нормированное пространство, полное в норме, порожденной скалярным произведением.

Теорема:  Для любого элемента гильбертова пространства существует единственный элемент наилучшего приближения в конечномерном подпространстве гильбертова пространства.

Определение:  L плотное в E, если "xÎE $uÎL: ║x-u║0 $ конечная e-сеть

Теорема:  Арцела.  MÌC[a,b] компактно ó все элементы множества равномерно ограничены и равностепенно непрерывны.

Определение:  Компактный (вполне непрерывный) оператор – замкнутый шар пространства X переводит в замкнутый шар пространства Y.

Определение:  s(X,Y) – подпространство компактных операторов

Теорема:  Шаудера. AÎs(X,Y) ó A*Îs(X*,Y*)

Линейные нормированные пространства

Пространства векторов

              сферическая норма

                          кубическая норма

                                        ромбическая норма

                        p>1

Пространства последовательностей          

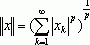                                                   p>1

          или             пространство ограниченных последовательностей

                     пространство последовательностей, сходящихся к нулю

                       пространство сходящихся последовательностей