Применение графиков в решении уравнений

Основная часть:    

            

 Применение графиков в решении уравнений.

 I)Графическое решение квадратного уравнения:

Рассмотрим приведённое квадратное уравнение : x2+px+q=0;

Перепишем его так:x2=-px-q.(1)

Построим графики зависимостей:y=x2 и y=-px-q.

График первой зависимости нам известен, это есть парабола; вторая зависимость- линейная; её график есть прямая линия. Из уравнения (1) видно, что в том случае, когда х  является его решением, рдинаты точек обоих графиков равны между собой. Значит, данному значению х соответствует одна и та же точка как на параболе, так и на прямой, то есть парабола и прямая пересекаются в точке с абциссой х.

Отсюда следующий графический способ решения квадратного уравнения:чертим параболу у=х2, чертим(по точкам) прямую       у=-рх-q.

Если прямая и парабола пересекаются, то абциссы точек пересечения являются корнями квадратного уравнения. Этот способ удобен, если не требуется большой точности.

Примеры:

1.Решить уравнение:4x2-12x+7=0

Представим его в виде x2=3x-7/4.

Построим параболу y=x2 и прямую y=3x-7/4.

Рисунок 1.

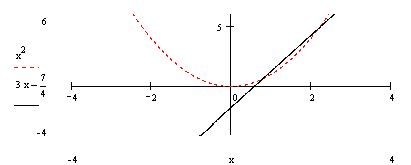
Для построения прямой можно взять, например, точки(0;-7/4) и (2;17/4).Парабола и прямая пересекаются в двух точках с абциссами x1=0.8 и x2=2.2 (см. рисунок 1).

2.Решить уравнение : x2-x+1=0.

Запишем уравнение в виде: x2=x-1.

Построив параболу у=х2 и прямую у=х-1, увидим, что они не пересекаются(рисунок 2), значит уравнение не имеет корней.

Рисунок 2.

 

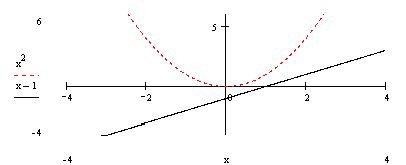
Проверим это. Вычислим дискриминант:

                        D=(-1)2-4=-3<0,

А поэтому уравнение не имеет корней.

Рекомендуем скачать другие рефераты по теме: сочинение на тему онегин, решебник по русскому.





1  2  3  4 | Следующая страница реферата