Принцип Дирихле
| Категория реферата: Рефераты по математике
| Теги реферата: бесплатные доклады, где диплом
| Добавил(а) на сайт: El'chenko.
Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата
По-другому его можно сформулировать так:
"Если среднее арифметическое нескольких чисел больше a, то хотя бы одно из этих чисел больше a";
или в терминах "зайцев":
"Если n кроликов съели m кг травы, то какой-то кролик съел не меньше m/n кг травы".
Кроме того, существует простая геометрическая интерпретация непрерывного принципа Дирихле:
"Пусть из некоторой точки на плоскости проведено N различных лучей; тогда угол между некоторыми двумя из них не менее 360°/N".
Понятно, что если рассматривать только углы между соседними лучами, то всего получится N углов (См. рисунок). В сумме они составляют полный угол, равный 360°. Следовательно,
по непрерывному принципу Дирихле градусная мера одного из этих углов не менее 360°/N (иначе их сумма будет меньше 360°).
Рассмотренный принцип называется непрерывным постольку, поскольку здесь числа (или градусные меры углов) могут принимать любое значение из некоторого промежутка, в то время как принцип Дирихле в обычном смысле оперирует с дискретным набором объектов ("зайцев")- было бы абсурдным предполагать, что в клетке может оказаться, скажем, два с половиной зайца.
Пример
17. На плоскости дано n попарно непараллельных прямых. Доказать, что найдутся
две из них, угол между которыми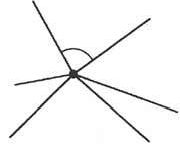
не меньше 180°/n.
Указание. Достаточно перенести прямые параллельно самим себе так, чтобы все они проходили через одну точку. Из этой точки будет выходить 2n лучей, и теперь можно применить принцип Дирихле.
Пример 18. На полях шахматной доски 8×8 расставлены действительные числа, каждые два из которых отличаются не менее чем на 1/9. Доказать, что есть пара соседних (имеющих общую сторону) клеток, разность чисел в которых не меньше 1/2.
Решение Пусть A- наименьшее из выписанных на доске чисел, а B- наибольшее. Покажем, что B-A і7.
Запишем числа в порядке возрастания (заметим, что никакие два числа не равны):
|
(здесь x1 = A, x64 = B).
Тогда
|
|
|
Допустим теперь, что утверждение задачи неверно, т.е. в любой паре соседних клеток числа отличаются меньше чем на 1/2. Рассмотрим две клетки, в которых записаны числа A и B. Понятно, что, переходя из клетки в клетку, можно попасть из клетки A в клетку B, сделав не более 14 переходов. Самый худший случай, когда нужно сделать ровно 14 переходов, показан на рисунке (A, B- противоположные клетки). По предположению приращение на каждом переходе меньше 1/2. Поэтому B - A < 14·(1/2) = 7. Противоречие.
Список литературы
[1] Андреев А.А., Горелов Г.Н., Люлев А.И., Савин А.И. "Принцип Дирихле", Самара "Пифагор", 1997г
[2] И. Л. Бабинская. Задачи математических олимпиад. М.: Наука, 1975.
[3] Д. X. Муштари. Подготовка к математическим олимпиадам: задачи, темы, методы. Казанский ун-т, 1990.
[4] В. В. Прасолов. Задачи по планиметрии. Ч. 2. М.: Наука, 1991.
Рекомендуем скачать другие рефераты по теме: государство курсовая работа, культура скачать реферат.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата
Главная