Предыдущая страница реферата | 1  2  3  4  5  6



Если условие не выполняется, то седловая точка отсутствует и требуется реализация смешанной стратегии.

Решение в смешанных стратегиях состоит в реализации чистых стратегий с различными вероятностями, задаваемыми распределением:

для проектируемого изделия в виде вектора-столбца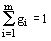

G = {gi}, где i = 1,2 ...m; ;

для противодействия в виде вектора-строки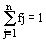

F = {fj}, где j = 1,2 ...n;

, где

gi - вероятность выбора стратегии ui;

fj - вероятность выбора стратегии vj.

Платежную функцию запишем в следующем виде:

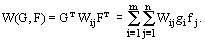, где индексом "т" обозначена процедура транспонирования.

Платежная функция W(G,F) всегда имеет седловую точку, т.е. всегда существует решение матричной игры. Это утверждение соответствует основной теореме теории матричных игр: каждая матричная игра с нулевой суммой имеет, по крайней мере, одно решение в чистых или смешанных стратегиях.

Последовательность решения игры следующая:

Анализируется платежная матрица на предмет исключения заведомо невыгодных и дублирующих стратегий. Проверяется наличие седловой точки по условию седловой точки. Если решение в чистых стратегиях отсутствует, то ищется решение в смешанных стратегиях с помощью методов линейного программирования или методом Монте-Карло. Литература. Андреев В.Н., Герасимов Ю.Ю. Принятие оптимальных решений: Теория и применение в лесном деле. Йоэнсуу: Из-во ун-та Йоэнсуу, 1999. 200 с. Беллман Р., Калаба Р. Динамическое программирование и современная теория управления. М.: Наука, 1969. 120 с. Вентцель Е.С. Элементы динамического программирования. М.: Наука, 1964. 176 с. Вентцель Е.С. Исследование операций: задачи, принципы, методология. М.: Наука, 1988. Калихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах. М.: Высшая школа, 1979. 125 с. Кузнецов А.В., Холод Н.И., Костевич Л.С. Руководство к решению задач по математическому программированию. М.: Вышэйшая школа, 1978. 256 с. Курицкий Б.Я. Оптимизация вокруг нас. Л.: Машиностроение, 1989. 144 с. Киреева А.Я., Трошин Л.И. Сборник задач по математическому программированию. М.: МЭСИ, 1968. 168 с. Жак С.В. Математическое программирование. Нелинейные и стохастические задачи. Ростов-на-Дону: РГУ, 1972. 90 с. Злобинская Э.А. Методические указание по математическому программированию для студентов экономических специальностей. Часть 1. Барнаул: АСХИ, 1980. Редькин А.К. Основы моделирования и оптимизации процессов лесозаготовок. М.: Лесная промышленность, 1988. 256 с. Реклейтис Т. Оптимизация в технике. М.: Мир. Т. 1. - 279 с. Т. 2. - 320 с. Юдин Д.Б. Задачи и методы стохастического программирования. М.: Сов. радио, 1979. 392 с. Davis L.S., Johnson K.N. Forest management. New York: McGraw-Hill Book Company, 1987. 790 с. Моисеев Н.Н., Математические методы системного анализа М. Наука 1981 487 с. Е.С.Вентцель Исследование операций. Задачи, принципы, методология. М. Наука 1988 206 с.
Скачали данный реферат: Jugancev, Ливия, Simona, Сиянков, Адриана, Aboimov.
Последние просмотренные рефераты на тему: реферат способы, контрольные по геометрии, конспект урока 9 класс, решебник 10 11.





Предыдущая страница реферата | 1  2  3  4  5  6