Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Возведём две новые переменные  и , тогда ,

.

Заметим, что .

В итоге получим систему уравнений:

  

Используя первоначальные уравнения системы, преобразуем вторые, заменив первую скобку единицей, а вторую подставим вместо неизвестного у выражение , также полученное из первого .

Приведём подобные члены, раскрыв предварительно скобки и решив полученное квадратное уравнение. Его корни  и . Вернёмся теперь к начальной подстановке и получим искомые решения:

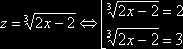
Введение нового неизвестного.

Решив эти уравнения, найдём радикалы более высоких степеней, но наиболее часто использовавшийся способ их решения – введение нового(новых) неизвестного.

Пример 2.

 

Обозначим , тогда

а)

Уравнение примет вид:

Корень  не удовлетворяет условию  

Ответ: 76.

Методы решения иррациональных уравнений.

Методы решения иррациональных уравнений, как правило основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному, либо является его следствием. Поэтому существуют два пути при решении иррациональных уравнений:

1) переход к выводным уравнениям (следствиям) с последующей проверкой корней;

2) переход к равносильным системам.

Второй подход избавляет от подстановки полученных корней в исходное уравнение (иногда такую проверку осуществить нелегко) и, вообще говоря, является более предпочтительным. Однако если в ходе решения оказалось, что проверка полученных корней не представляет труда, то можно не выяснять источники появления посторонних корней и не переходить к равносильным системам.

Пример 1.

Возведём в 6 степень:

Рекомендуем скачать другие рефераты по теме: реферат на тему рынок, курсовые.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата