Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

Отметим, что в двойственной задаче переменные yi могут быть и отрицательными.

Рассмотрим в качестве исходной задачу (2.12), (2.13). С учетом (7.1) и (7.7) запишем

С = (120, 100, 150, 0, 0, 0, 0, 0), B = (, , , , ),

.

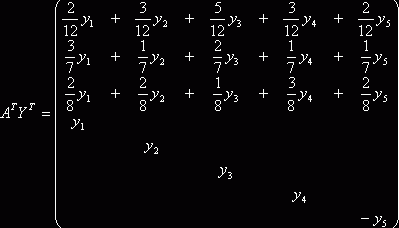Двойственная задача имеет вид

;    (7.8)

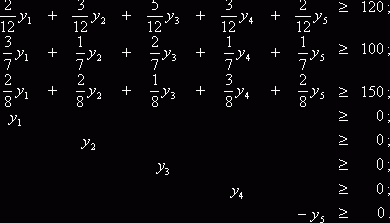                     (7.9)

8. Формирование оптимального решения двойственной задачи на основе теоремы о двойственности

Оказывается, что для задач (7.2) - (7.4) и (7.5), (7.6), называемых двойственной парой, справедлива следующая теорема.

Теорема (первая теорема о двойственности). Если одна из задач двойственной пары (7.2) - (7.4) и (7.5), (7.6) имеет решение, то другая задача также разрешима. При этом для любых оптимальных планов  и (здесь Мх, Му – множества планов соответственно прямой и двойственной задач) задач (7.2) - (7.4) и (7.5), (7.6) имеет место равенство

.                                                                                

Если линейная форма одной из задач не ограничена (для F(X) – сверху, для f(Y) - снизу), то другая задача не имеет ни одного плана.

Оптимальное решение двойственной задачи может быть найдено на основе следующего следствия из этой теоремы.

Следствие. Если вектор  является оптимальным опорным планом задачи (7.2) - (7.4), то вектор  (8.1), является оптимальным опорным планом задачи (7.5), (7.6).

Стоит отметить, что в ходе решения исходной задачи вторым алгоритмом, при каждом шаге вычисляется вектор . И если Х – оптимальный опорный план задачи (7.2) - (7.4), то в (m+1)-й строке, соответствующей основной таблице, находится решение задачи (7.5), (7.6).

Пусть двойственная задача имеет вид (7.8), (7.9).

Так как исходная задача (2.12), (2.13) имеет решение, то на основании рассмотренной теоремы о двойственности двойственная задача также разрешима.

Оптимальным опорным планом исходной является  (см. п.4, п.6). При этом

;

; .

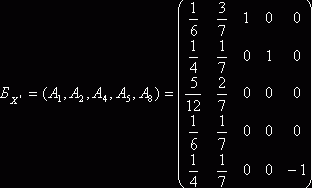Вычислим

.

На основании следствия из теоремы о двойственности можно заключить, что  является оптимальным планом двойственной задачи, при котором . Анализируя (m+1)-ю строку основной таблицы (см. табл. 6.3, шаг 5), можно убедиться в том, что оптимальный план двойственной задачи, сформированный на основе теоремы о двойственности, совпадает с оптимальным планом, найденном при решении исходной задачи вторым алгоритмом симплекс-метода. Это говорит о том, что оптимальный план задачи (7.8) - (7.9) найден верно.

9. Анализ результатов и выводы

В данной работе рассматриваются два способа решения исходной задачи линейного программирования.

Первый заключается в том, что сначала решается вспомогательная задача (L-задача), позволяющая построить начальный опорный план, затем на основе этого найденного плана решается исходная задача (определяется ее оптимальный план). Второй способ является объединением двух этапов и состоит в решении расширенной задачи (M-задачи), также приводящей к нахождению оптимального плана исходной задачи.

Рекомендуем скачать другие рефераты по теме: доклад по географии на тему, реферат предприятие.





Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата