Структура статистики объектов нечисловой природы

| Категория реферата: Рефераты по математике
| Теги реферата: рефераты, сочинение егэ
| Добавил(а) на сайт: Дедин.

Предыдущая страница реферата | 1 2 3 4 5 | Следующая страница реферата

1. 7) аксиоматическое введение метрик.

Перечисленные разделы тесно связаны друг с другом, как продемонстрировано, в частности, в работах [1, 4, 24]. Вне данного перечня остались работы по хорошо развитым классическим областям - статистическому контролю [11-14], таблицам сопряженности [34], а также по анализу текстов [35, 36] и некоторые другие [25-29]. Таким образом, рассмотрим постановки 1970-90 гг. вероятностной статистики объектов нечисловой природы.

. Статистика в пространствах общей природы

Пусть -элементы пространства , не являющегося линейным. Как определить среднее значение для ? Поскольку нельзя складывать элементы , сравнивать их по величине, то необходимы подходы, принципиально новые по сравнению с классическими. В работе [37] предложено использовать показатель различия (содержательный смысл: чем больше , тем больше различаются и ) и определять среднее как решение экстремальной задачи

. (1)

Таким образом - это совокупность всех тех , для которых функция

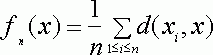
достигает минимума на .

Для классического случая при имеем: , а при среднее совпадает с выборочной медианой (при нечетном объеме выборки; а при четном - является отрезком с концами в двух средних элементах вариационного ряда).

Для ряда конкретных объектов среднее как решение экстремальной задачи вводилось рядом авторов. В 1929 г. Джини и Гальвани [38] применили такой подход для усреднения точек на плоскости и в пространстве (см. также [39]). Кемени [40-42] решение задачи (1) называл медианой или средним для выборки, состоящей из ранжировок. При моделировании лесных пожаров, согласно выражению (1), было введено "среднеуклоняемое множество" [43]. Общее определение среднего (1) рассмотрено нами в работах [2, 37].

Основной результат, связанный со средними (1) - аналог закона больших чисел. Пусть. - независимые одинаково распределенные случайные элементы со значениями в пространстве общей природы (определения здесь и далее - согласно Математической Энциклопедии [44]). Теоретическим средним, или математическим ожиданием, назовем [37]

. (3)

Закон больших чисел состоит в сходимости. к . при . Поскольку и эмпирическое, и теоретическое средние - множества, то понятие сходимости требует уточнения.

Одно из возможных уточнений таково [46]: для функции

(4)

введем понятие "-пятки" (>0)

. (5)

Очевидно, -пятка - это окрестность (если он достигается), заданная в терминах минимизируемой функции. Тем самым снимается вопрос о выборе метрики в пространстве (позже подобная идея была использована в работе [45]). Тогда при некоторых условиях регулярности для любого>0 вероятность события

(6)

стремится к 1 при. , т. е. справедлив закон больших чисел [46].

Естественное обобщение рассматриваемой задачи позволяет построить общую теорию оптимизационного подхода в статистике. Как известно [47], большинство задач прикладной статистики может быть представлено в качестве оптимизационных. Как себя ведут решения экстремальных задач? Частные случаи этой постановки: как ведут себя при росте объема выборки оценки максимального правдоподобия, минимального контраста (в том числе робастные в смысле Тьюки-Хьюбера [1, 48-50]), оценки нагрузок в факторном анализе и методе главных компонент при отсутствии нормальности, оценки метода наименьших модулей в регрессии [51] и т. д.

Обычно легко устанавливается, что для некоторых пространств и последовательности случайных функций. при. найдется функция такая, что