Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

В) Бинормальные 3х мерные моменты инерции (,) для (+P) и (-P) плотности на бинормали подвижного трехгранника Френе:

1в) - относительный интервал бинормального момента инерции -P плотности

2в) -относительный интервал бинормального момента инерции +P плотности

3в) абсолютный бинормальный момент инерции +P плотности

нормальный и касательный моменты инерции в соприкасающейся плоскости могут рассматриваться как производные (корни) от положительных и отрицательных бинормальных моментов: и, соответственно, могут принимать значения:;;;

4в) - относительный векторный бинормальный RL-момент инерции

где = - угол между и продолжением

5в) - относительный скалярный бинормальный RL-момент инерции

где = - угол между и продолжением

Кроме того, поскольку бинормальный момент является произведением нормального и касательного векторов, один из которых 3-мерный, бинормальный вектор представляется в его трехмерной проекции.

Г) Нормальное (действительное), касательное (мнимое) и бинормальное (комплексное) пространства 3-мерных x-подобных моментов.

1г) (, ,) – касательный x-подобный момент и его ХУZ-проекции

2г) () - нормальный x-подобный момент и его ХУZ -проекции

3г) ()- комплексный (результирующий) x-подобный момент и его ХУZ- проекции.

4г); 5г); 6г);

7г); 8г)

9г), при

10г), при

11г)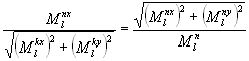; 12г)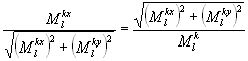

Рекомендуем скачать другие рефераты по теме: шпоры по гражданскому, предмет культурологии.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата