Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

выполнялось бы для всех х на отрезке [a,b].

Теорема. (Признак равномерной сходимости Вейерштрасса)

(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)

Ряд сходится равномерно и притом абсолютно на отрезке [a,b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :

т.е. имеет место неравенство:

.

Еще говорят, что в этом случае функциональный ряд  мажорируется числовым рядом .

ряд  называется положительным, если Un≥0, для всех n ? N

Интегральный признак Коши.

Если j(х) – непрерывная положительная функция, убывающая на промежутке [1;¥), то ряд j(1) + j(2) + …+ j(n) + … =  и несобственный интеграл  одинаковы в смысле сходимости.

Пример. Ряд 1 и расходится a£1 т.к. соответствующий несобственный интеграл 1 и расходится a£1. Ряд  называется общегармоническим рядом.

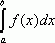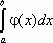Следствие. Если f(x) и j(х) – непрерывные функции на интервале (a, b] и  то интегралы  и  ведут себя одинаково в смысле сходимости.

Степенные ряды.

Определение. Степенным рядом называется ряд вида

.

Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.

Пример. Исследовать на сходимость ряд

Применяем признак Даламбера:

.

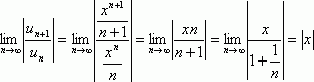Получаем, что этот ряд сходится при и расходится при .

Теперь определим сходимость в граничных точках 1 и –1.

При х = 1:  ряд сходится по признаку Лейбница (см. Признак Лейбница. ).

При х = -1:  ряд расходится (гармонический ряд).

1 теорема Абеля.

Рекомендуем скачать другие рефераты по теме: ответы гиа, отчет по производственной практике.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата