Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

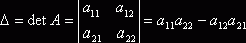   (1.9)

Формула (1.9) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы. Словесная формулировка этого правила такова: определитель второго порядка, соответствующий матрице (1.8), равен разности произведения элементов, стоящих на главной диагонали этой матрицы, и  произведения элементов, стоящих на побочной ее диагонали. Определители второго и более высоких порядков находят широкое применение при решении систем линейных уравнений.

Рассмотрим, как выполняются операции с матрицами в системе  MathCad. Простейшие операции матричной алгебры реализованы в MathCad в виде операторов. Написание операторов по смыслу максимально приближено к их математическому действию. Каждый оператор выражается соответствующим символом. Рассмотрим матричные и векторные операции MathCad 2001.  Векторы являются частным случаем матриц размерности n x 1,  поэтому для них справедливы все те операции, что и для матриц, если ограничения особо не оговорены (например, некоторые операции применимы только к квадратным матрицам n x n). Какие-то действия допустимы только для векторов (например, скалярное произведение), а какие-то, несмотря на одинаковое написание, по-разному действуют на векторы и матрицы.

При работе с матрицами используется панель инструментов “Матрицы”

Рис.1 Панель инструментов  Матрицы

Для ввода матрицы:

введите имя матрицы и знак присваивания (двоеточие)

щелкните по значку “создать матрицу” в панели “Матрицы”.

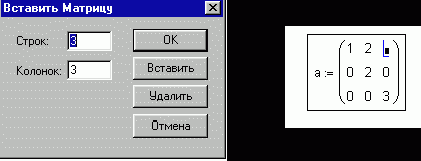В появившемся диалоге задайте число строк и столбцов матрицы.

После нажатия кнопки OK открывается поле для ввода элементов матрицы. Для того, чтобы ввести элемент матрицы, установите курсор в отмеченной позиции и введите с клавиатуры число или выражение.

Для того, чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно:

выделить матрицу и щелкнуть в панели по кнопке операции,

или щелкнуть по кнопке в панели и ввести в помеченной позиции имя матрицы.

Меню “Символы” содержит три операции - транспонирование, инвертирование, определитель.

Это означает, например, что вычислить определитель матрицы можно, выполнив команду Символы/Матрицы/Определитель.

Номер первой строки (и первого столбца) матрицы MathCAD хранит в переменной ORIGIN. По умолчанию отсчет ведется от нуля. В математической записи чаще принято вести отсчет от 1. Для того, чтобы MathCAD вел отсчет номеров строк и столбцов от 1, нужно задать значение переменной ORIGIN:=1.

Функции, предназначенные для работы с задачами линейной алгебры, собраны в разделе “Векторы и матрицы” диалога “вставить функцию” (напоминаем, что он вызывается кнопкой  на панели “Стандартные”). Основные из этих функций будут описаны позже.

Транспонирование

Рис.2  Транспонирование матриц

Транспортированием называют операцию, переводящую матрицу размерности mxn в матрицу размерности n x m, делая столбцы исходной матрицы строками, а строки — столбцами. Пример приведен в листинге на рис.2. Ввод символа транспонирования (transpose) осуществляется с помощью панели инструментов Matrix (Матрица) или нажатием клавиш +. He забывайте, что для вставки символа транспонирования матрица должна находиться между линиями ввода. Напоминание о линиях ввода по отношению к матрицам приведено ранее.

Сложение

В MathCAD можно как складывать матрицы, так и вычитать их друг из друга. Для этих операторов применяются символы или соответственно. Матрицы должны иметь одинаковую размерность, иначе будет выдано сообщение об ошибке. Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых.

Кроме сложения матриц, MathCAD поддерживает операцию сложения матрицы со скалярной величиной, т.е. числом (пример на рис.4). Каждый элемент результирующей матрицы равен сумме соответст-вующего элемента исходной матрицы и скалярной величины.

Рис.5   Смена знака матрицы

Результат смены знака матрицы эквивалентен смене знака всех ее элементов. Для того чтобы изменить знак матрицы, достаточно ввести перед ней знак минуса, как перед обычным числом  (пример на рис.4).

Умножение

При умножении следует помнить, что матрицу размерности m x n допустимо умножать только на матрицу-размерности n x p (р может быть любым). В результате получается матрица размерности m х р.

Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой или воспользоваться панелью инструментов Matrix (Матрица), нажав на ней кнопку Dot Product (Умножение) (рис.1). Умножение матриц обозначается по умолчанию точкой, как показано в примере на рис 6. Символ умножения матриц можно выбирать точно так же, как и в скалярных выражениях.

Рекомендуем скачать другие рефераты по теме: сообщение, ответы 5 класс.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата