|
3 |
9 |
34,2 |
8 |
85,76 |
119,96 |
|
4 |
9 |
96,48 |
7 |
26,6 |
123,08 |
Выбирается тот комплект машин, который обеспечивает максимальную производительность, в пределах условия m1"*Па+m2"*Па>Пэ на 20%. Этому условию удовлетворяет вариант
Экскаватор с объемом ковша 1,00
12 автосамосвалов грузоподъемностью 10 т на маршрут Е1-Е10;
9автосамосвалов грузоподъемностью 10 т на маршрут Е1-Е11;
2.5. Определение оптимального потока материалов в сети
2.5.1. Расчет пропускных способностей ребер транспортной сети
Cij*=Cij, если 0<xij<bij;
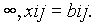
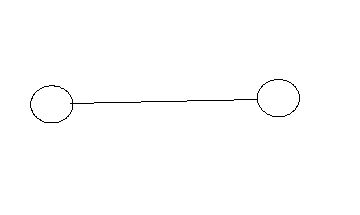
Схема 4. Пропускные способности сети.
Пропускные способности отдельных участков сети определяются исходя из рассчитанной выше суммарной производительности потоков автосамосвалов, идущих по этим участкам сети.
Пропускная способность вычисляется по формуле:
bij=mik*Паik*kа,
где bij - пропускная способность по ребру между двумя пунктами, м3/час
к - число маршрутов;
ka - коэффициент перевыполнения (1,15-1,20);
Пропускная способность ребер, через которые одновременно проходят несколько маршрутов, представляет собой сумму пропускных способностей каждого из этих маршрутов.
Ниже представлен список маршрутов и соответствующих им пропускных способностей.
Е1Е10 - 55м3/час
Е1Е11 - 48м3/час
Е2Е10 - 95,4м3/час
Е3Е11 - 180м3/час
Транспортная сеть с нанесенными на ней пропускными способностями и стоимостями перевозок представлена на схеме 3..
2.5.2. Определение потока минимальной стоимости (задача Басакера-Гоуэна)
Постановка задачи: задана сеть с одним истоком Е0 и одним стоком Е12, и промежуточными вершинами Е1-Е11. Каждому ребру поставлены в соответствие две величины: пропускная способность bij и дуговая стоимость Cij (стоимость доставки единицы потока по ребру Еij). Необходимо найти поток из источника в сток заданной величины В, обладающий минимальной стоимостью.
Целевая функция:
F = 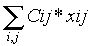 ®
min
®
min
Ограничения:
0£
x £
bij, i ¹
j, i, j = 0,n
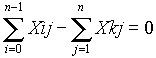 — закон сохранения потока
— закон сохранения потока
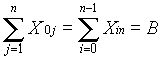 — поток, идущий из источника, равен потоку, входящему в сток, и равен максимальному потоку в сети.
— поток, идущий из источника, равен потоку, входящему в сток, и равен максимальному потоку в сети.
При наличии ограничений на пропускные способности ребер можно последовательно находить различные пути минимальной стоимости и пропускать по ним поток до тех пор, пока суммарная величина потока по всем путям не будет равна заданной величине потока.
Алгоритм Басакера-Гоуэна
Положим все дуговые потоки равными нулю (Xij=0).
Находим в сети путь с минимальной стоимостью и определяем модифицированные дуговые стоимости Cij, зависящие от величины найденного потока следующим образом:
Рекомендуем скачать другие рефераты по теме: банк бесплатных рефератов, доклад на тему.
Предыдущая страница реферата |
5
6
7
8
9
10
11
12
13
14
15 |
Следующая страница реферата

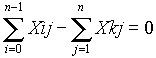 — закон сохранения потока
— закон сохранения потока
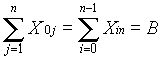 — поток, идущий из источника, равен потоку, входящему в сток, и равен максимальному потоку в сети.
— поток, идущий из источника, равен потоку, входящему в сток, и равен максимальному потоку в сети.
 Главная
Главная