Предыдущая страница реферата | 1  2  3  4



ПРИЛОЖЕНИЕ 1. ПОЛНОЕ РЕШЕНИЕ АСПЕКТНОЙ СИСТЕМЫ НЕРАВЕНСТВ Нагайцев А.Н., г. Симбирск, УлГУ

Мы будем решать “аспектную” систему неравенств:
-E < D*Vл - Nл < E
-E < D*Vм - Nм < E
-E < D*Vю - Nю < E
-E < D*Vс - Nс < E
полным перебором на компьютере. Для выбора способа решения примем во внимание такие соображения: алгоритм должен быть, во-первых, понятным и легко реализуемым, а во-вторых, он должен работать приемлемое время на любом современном компьютере. Понятно, что полным перебором по D, Nл, Nм, Nс, Nю мы добьёмся малого, так как общее число вариантов перебора 2000*365,25*937*1832*1933*24738. Машина, перебирающая, например, миллион вариантов в секунду, будет работать чуть больше 1,9 миллиона лет.

Глядя на систему, можно сразу сказать следующее: переменная D является общей для всех неравенств системы, и поэтому логично начинать перебор именно по ней. Сделаем так: в цикле по возрастанию для D будем решать каждое из неравенств, после чего сформируем общее решение и запомним его. Находить решение каждого неравенства будем, зная, что величина Е меньше единицы (и даже половины). Можно округлять выражение D*Vx до ближайшего целого, которое примем за Nx. Найдем после этого Е как модуль разности D*Vx-Nx. После того как найдем решения каждого отдельного неравенства, найдем общий орб, как наибольший из орбов для всех неравенств. Полученное решение станем запоминать, если орб системы окажется меньше заранее заданного максимума. Таким образом, мы получим общую картину решений, которую можно отразить графически - см. следующий рисунок, или таблично. Вот что выходит, если отложить годы, соответствующие решениям D системы по горизонтальной оси, а соответствующие орбы - по вертикали:

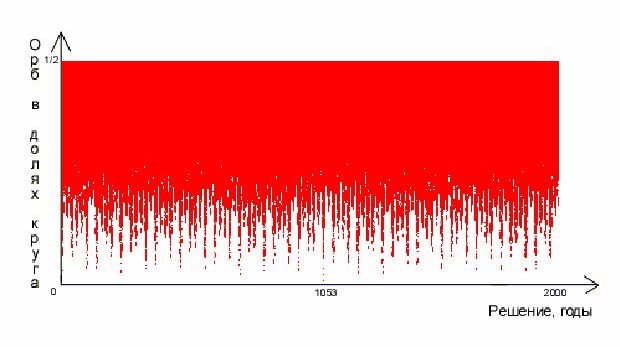
Рис. 3 Общий график решений аспектной системы неравенств.

Конечно, этот рисунок не претендует на на отчётливость демонстрации, в первую очередь из-за сложности отображения большого множества решений, но он может проиллюстрировать некоторые выводы. Например, мы видим, что при орбе порядка 100 градусов любые дни являются решениями системы. Так же отчетливо видно, что наилучшим решением являются 1053 года (полная таблица ниже). Увеличим нижнюю часть рисунка, соответствующую решениям системы при малых орбах. Наиболее разумно ограничиться 15 градусами, поскольку такой орб бывает при разбросе в один знак Зодиака. Крестик отмечает наилучшего представителя в своей вертикальной полосе решений:

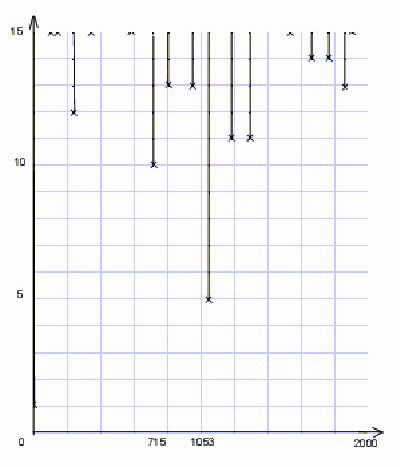
Рис.4 График решений при орбе 15 градусов (компактный фрагмент Рис.3)

Решение Орб	в днях	в юлианских годах
	384518	1052 года + 275 дней
10	261257	715 лет + 103 дня
11	435192 471869	1191 год + 179 дней 1291 год + 331 день
12	87351	239 лет + 56 дней
13	297166 348609 681685	813 лет + 217 дней 954 года + 160 дней 1866 лет + 128 дней
14	347840 609099 645776	952 года + 121 день 1667 лет + 227 дней 1768 лет + 13 дней
15	35908 50675 123260 210611 558452 696450	98 лет + 113 дней 138 лет + 269 дней 337 лет + 170 дней 576 лет + 227 дней 1528 лет + 349 дней 1906 лет + 283 дня

Таблица 1. Решения для орбов менее 15 градусов:

Что же интересного можно увидеть в этой таблице? Во-первых, хочется отметить появление нового очень интересного решения, которое не встречается у А.Б. Верёвкина выше: 715 лет. Этот квазипериод соответствует хронологическому сдвигу между Третьей Римской Империей и Священной Римской Империей X - XIII веков, причём орб у этого решения не большой - только 10 градусов. В этой таблице мы встречаем все хронологические сдвиги, найденные А.Т. Фоменко и Г.В. Носовским, за исключением 400 летнего русского и 360 летнего европейского [15, Приложение II], которые могут иметь иную, неастрологическую природу возникновения.

Приведу в заключение фрагмент программы, которая находит решения аспектной системы неравенств. Программа написана на языке Delphi. Полный обсчет системы производится за 20 секунд на машине CPU - Thunderbird 850.

for d:=0 to maxD do // - цикл по дням
begin
eps:=0.0;
M:=round(D*Vm); // - находим решение по Марсу
epsM:=abs(D*Vm-M); // - его орб
if epsM>eps then eps:=epsM; // - и, возможно, он наибольший
J:=round(D*Vj);
epsJ:=abs(D*Vj-J);
if epsJ>eps then eps:=epsJ;
S:=round(D*Vs);
epsS:=abs(D*Vs-S);
if epsS>eps then eps:=epsS;
L:=round(D*Vl);
epsL:=abs(D*Vl-L);
if epsL>eps then eps:=epsL;
if eps
begin
// Запоминаем решение
end;
end;

ЛИТЕРАТУРА

Лурье Ф.М. "Российская и мировая история в таблицах",- СПб, Каравелла, 1995. Фоменко А.Т. "Методы статистического анализа нарративных текстов и приложения к хронологии",- М., изд. МГУ, 1990. Морозов Н.А. "Христос, т. I. Небесные вехи земной истории человечества",- М., Крафт+Леан, 1997. Носовский Г.В., Фоменко А.Т. "Реконструкция всеобщей истории. Исследования 1999 - 2000 годов",- М., ФИД Деловой Экспресс, 2000. Фоменко А.Т. "Критика традиционной хронологии античности и средневековья (какой сейчас век?) Реферат",- М., изд. МГУ, 1993. Жабинский А.М. "Другая история искусства",- Вече, 2001. "Христианство. Энциклопедический словарь в 3-х томах", под ред. С.С. Аверинцева,- М., БРЭ, 1993. Олдос Хаксли "Луденские бесы",- М., Терра, 2000. "Эзотерика, том II. Астрология",- М., Воскресенье, 1993. Бардо Кидого "Ключи к пророчествам Нострадамуса",- М., Терра, 2000. Леманн А. "Иллюстрированная история суеверий и волшебства от древности до наших дней", - К., Украiна, 1993. Колесов Е.Н. (Het Monster) "Индийская астрология",- Д., Сталкер, 1997. Морозов Н.А. "Христос, т. IV. Во мгле минувшего при свете звёзд",- М., Крафт+Леан, 1998. Постников М.М. "Критическое исследование хронологии древнего мира, т. I. Античность",- М., Крафт+Леан, 2000.

Носовский Г.В., Фоменко А.Т. "Реконструкция всеобщей истории, книга 1", - М., ФИД Деловой Экспресс, 2000.

Скачали данный реферат: Касьяненко, Pjatosin, Kemoklidze, Альбина, Киселев, Filippa.
Последние просмотренные рефераты на тему: операции реферат, реферат знания, реферат поведение, ответ 3.





Предыдущая страница реферата | 1  2  3  4