Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Выбираем fд = 800 Гц. Отсюда после нормирования частот W =

ПП ® [0; 0,25], ПН ® [0,375; 0,5].

Здесь Н(0) № 0, поэтому фильтр симметричный.

H(0,5wд) = 0, поэтому N - четное.

Следовательно, требуемую АЧХ необходимо продолжить на диапазон [0,5wд; wд] нечетным образом (Рис. 3.8, а).

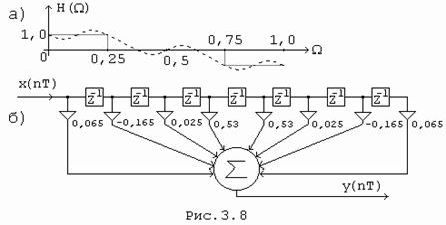
Расчет начинается с выбора величины N.

Пусть N = 8. Отсюда интервал между выборками W1 = = 0,125.

Формула для ФЧХ (3.3): j(w) = -wT . Отсюда

j (W) = -7pW, или для частот выборки j (kW1) = -7pW1,

Отсчеты АЧХ - по требуемой АЧХ на графике Рис. 3.8, а.

Следовательно, комплексные частотные отсчеты:

Н(jkW1) = {1e j0; 1e -j0,875p ; 1e -j1,75p ; 0; 0; 0; -1e -j5,25p ; -1e -j6,125p }

Отсюда расчет импульсной характеристики по формуле обр. ДПФ

h (nT) = 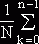H (jkW1) e j (2p/N) kn =

={0,065; -0,165; 0,025; 0,53; 0,53; 0,025; -0,165; 0,065}

что соответствует схеме фильтра на Рис. 3.8, б

Расчетная формула АЧХ такого типа фильтра - (3.5).

Поэтому Н(W) = 1,06 cos pW + 0,05 cos 3pW - 0,33 cos 5pW + 0,13 cos 7pW

Результаты расчета реализованной АЧХ приведены на графике Рис. 3.8, а (штриховая линия).

В окрестности точек разрыва требуемой АЧХ (в данном примере это частоты 0,25 и 0,75) отклонение от нормы реализованных характеристик получается значительным вследствие влияния эффекта Гиббса. Ослабить влияние эффекта Гиббса удается введением весовой функции (метод взвешивания) к импульсной характеристике.

Новая импульсная характеристика формируется по правилу:

h' (nT) = W (nt) * h (nT)

Где W (nT) - весовая функция или "сглаживающее окно".

Находят применение различные типы окон, например "окно" Хэмминга:

Рекомендуем скачать другие рефераты по теме: информация реферат, доклад по физкультуре.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата