Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Таким образом, решение уравнения (4.1) будет единственным, если ранг матрицы  равен M или ранг G матрицы равен M. Это верно, если выполняется следующее условие, которое в дальнейшем для краткости будем называть как

Первое ранговое условие:

T в матрице  все M столбцов линейно независимы,

T в матрице  есть не менее M линейно независимых строк.

Если выполняется первое ранговое условие, решение уравнения (4.1) единственно, выполняется условие (1) и для строки S не существует линейно зависимых строк, то это решение имеет вид

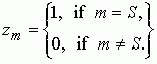         (4)

Отсюда и из (5.4) следует, что

 ,

т.е. все потенциалы х принимают булевские значения, что и требовалось показать. Итак, для этого должно выполнятся

Второе ранговое условие:

T в матрице  все M столбцов линейно независимы,

T в матрице  все строки линейно независимы.

7. Таблица истинности для схемы АД

Из вышесказанного следует, что достаточное условие существования булевского решения для обратного включения заключается в следующем:

1. матрица G удовлетворяет ранговому условию;

2. вектор у совпадает с одной из строк матрицы G;

3. все элементы AnAND соединены со всеми элементами AnNOT (математически это означает, что матрица B является бинарной);

4. любое  в матрице В должно принимать оба значения v 0 и 1 (в любом столбце матрицы В должен присутствовать и 0, и 1).

Схему АД будем описываеть таблицей, которая имеет вид, где матрицы B и G удовлетворяют вышеперечисленным условиям.

Будем называть схему АД булевской, если она удовлетворяет условиям 1) и 3), а вектор у, совпадающий с одной из строк матрицы G, будем называть правильным вектором. Булевская схема АД, на которую подан правильный вектор y, имеет булевское решение.

Булевская схема АД описывается таблицей истинности, которая имеет вид. При булевском решении

  

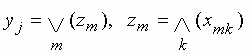
или

   .

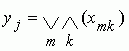Последнее выражение есть дизъюнктивная нормальная форма - ДНФ. Таким образом, схема АД, удовлетворяющая указанным условиям, удовлетворяет, кроме того, системе уравнений

Рекомендуем скачать другие рефераты по теме: реферат на тему экономика, курсовики скачать бесплатно.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата