Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Рис. 2

Здесь на первом графике представлен сигнал (синусоидальная несущая волна, модулированная синусоидальным сигналом малой частоты, то есть ) на выходе из передатчика (при Х = 0). На втором и третьем графиках представлено положение волн на расстояниях и от передатчика.

Очевидно, что при х = 0 все три волны совпадают по фазе. Далее они начинают “расходиться”. Это значит, что первая боковая, для которой начинает отставать по фазе от несущей, а вторая боковая, для которой – опережать.

Фазовый сдвиг боковой относительно несущей может быть определен по формуле:

, где – угловая частота несущей, - угловая частота модуляции (), х – расстояние, пройденное сигналом (длина линии), с – скорость света в вакууме, - производная зависимости коэффициента преломления от частоты . При этом считалось, что . Таким образом, происходит “фазовое уширение сигнала” равное (при линейной зависимости ). При дальнейшем уширении импулса он полностью деформируется (распадается) и при фазовом сдвиге, равном 2π, форма сигнала (синусоидального) будет повторена. Если “выделить” центр импульса (чем не характерная точка!), то совершенно очевидно, что скорость распостранения сигнала будет равна ФАЗОВОЙ СКОРОСТИ НЕСУЩЕЙ ВОЛНЫ! Очевидно также, что ПОНЯТИЯ “ГРУППОВОЙ СКОРОСТИ” НЕ СУЩЕСТВУЕТ! Существует только “уширение сигнала”, которое и ограничивает скорость предачи данных и длину линии в дисперсной среде.

Кроме того, совершенно очевидно, что КАЖДАЯ ИЗ СОСТАВЛЯЮЩИХ этого “волнового пакета” является монохроматической волной и НЕСЕТ СВОЮ ДОЛЮ ЭНЕРГИИ! А “понятие” “скорости распостранения энергии поля (?) этого импульса” (стр. 430 книги [1]) является странным и совершенно бессмысленным.

Возвращаясь к биению двух частот. Если сложить ДВЕ волны с близкими частотами и выделть (как сделал Рэлей с Ландсбергом) точку на биениях с максимальной амплитудой, то, очевидно, что эта точка будет слегка отставать () от первой волны (или опережать вторую). В случае же ТРЕХ волн точка с максимальной амплитудой, выделенная на биениях первой волны с несущей (центральной) будет опережать несущую, а точка на биениях второй волны с несущей будет на столько же отставать. При этом середина импульса и, соответственно, точка импульса с максимальной амплитудой будет распостраняться с ФАЗОВОЙ СКОРОСТЬ НЕСУШЕЙ ВОЛНЫ!

Проблема распостранения сигнала в дисперсной среде имеет важное практическое значение. В частности, с ней вплотную сталкиваются специалисты, работающие с волоконно-оптическими линиями связи. В таких линиях при передаче аналогового сигнала его “уширение” проявляется как искажения сигнала и, на некотором расстоянии от источника сигнал становится нераспознаваемым. При цифровой же передаче данных (модуляция осуществляется прямоугольными импульсами) “уширение сигнала” в меньшей степени влияет на передачу информации. Влияние дисперсной среды на цифровую передачу данных проиллюстрировано на Рис. 3.

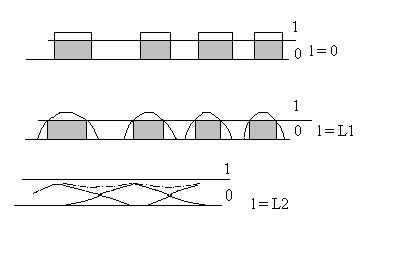
Рис. 3

Можно видеть, что сигнал читается и в случае “уширенного импульса” (средний график), так как а нем присутствуют уровни единица-нуль. Приемник же нормализует сигнал, превращая его опять в прямоугольный. И вобще, если кто-нибудь видел на осциллографе форму цифровых сигналов ЭВМ, тот знает, что эти сигналы – совсем не прямоугольные, а ближе к отрезку синусоиды. Таким образом, для предачи цифровой информации форма сигнала совершенно не обязательно должна поддерживаться прямоугольной. Очевидно также, что наличие “составляющих сколь угодно высоких частот с ничтожно малой амплитудой”, даже сильно опережающих или отстающих от несущей и полностью с ней рассинхронизированых будут проявляться как шумы и на сигнал не скажутся никак!

При дальнейшем удалении от источника, импульсы начинают перекрываться (нижний график) и, вот тогда уже сигнал не читается. Очевидно, что расстояние, на котором импульсы перестают читаться зависит от расстояния между импульсами, то есть от частоты модуляции.

Таким образом, для оптической линии важную роль играет произведение . То есть, по одной и той же линии можно передать данные с высокой скоростью (в бит/сек, не путать со скоростью распостранения сигнала!) на короткое расстояние или с малой скоростью – на большие расстояния. Кроме того, дисперсия материала линии также влияет на параметры линии – при больших значениях сокращается допустимая длина линии или скорость передачи данных.

Теперь оценим возможную длину дисперсной оптической линии по формуле, задавшись ее параметрами и допустимым уширением сигнала.

Предположим, что допустимое фазовое уширение сигнала () не должно превышать 0.1 рад (5,7 град). Зависимость дисперсии от длины волны возьмем из Рис. 28.3 стр. 542 книги [1] для области аномальной дисперсии раствора цианина. Тогда при длине волны 600 нм ( 1/сек). Предположим, что скорость передачи информации составляет 1000 бт/сек, то есть частота модулирующего сигнала будет порядка 1 КГц (). Подставляя эти значения в вышеприведенную формулу, получим допустимую длину оптической линии, которая получается равной 200 метрам. Здесь надо отметить, что зависимость n = f (ω) для захоложенных газов (сверхсветовые скорости получены, как раз, в таких средах) может быть существенно круче. Если, например, крутизна зависимости n = f (ω) будет на порядок выше, чем в приведенном примере, то допустимая длина линии пропорционально уменьшится до 20 метров.

Таким образом, в среде с любой дисперсией можно передать информацию, но ее скорость и длина линии зависит от дисперсии.

Кроме того, абсолютно очевидно, что если все три частоты, , и укладываются в область с n < 1, то и сигнал и энергия будут распостраняться со сверхсветовой скоростью!

3. Сверхсветовая скорость

Возвращаясь к “групповой скорости” - в сноске на стр. 430 книги [1], приводятся очень оригинальные рассуждения, относящиеся уже к сверхсветовым скоростям:

“При введении понятия групповой скорости мы ограничились случаем не очень большой дисперсии, ибо в противном случае импульс быстро деформируется и понятие групповой скорости теряет смысл. Так, например, вблизи полосы поглащения вещества, где фазовая скорость очень сильно меняется с частотой, формула (125.1) могла бы дать для U значение большее скорости света в вакууме, или отрицательное значение. В этой области наша формула неприложима. Энергия импульса распостраняется со скоростью, которую можно назвать скоростью сигнала; она, как показывает специальное исследование, вне указанной области совпадает с групповой скоростью, а внутри ее остается меньше скорости света в вакууме (??? выделено Г. И.)”. Вот так вот! Не больше не меньше!

Выходит, что, даже несмотря на то, что, понятие “групповой скорости” позволяет (правда, как было показано выше, весьма вольно и ошибочно) манипулировать скоростью передачи информации и энергии, но и этого, оказывается, мало! Не может превышать и все тут! И что это за “специальное исследование”? Таким образом, понятие рэлеевой “групповой скорости”, столь часто используемое для “доказательства” отсутствия сверхсветовых скоростей, также не дает основания утверждать, что в областях с n < 1 скорость не может преышать скорость света в вакууме! Выражаясь проще, не надо привлекать сюда “групповую скорость” - она не имеет никакого отношения к вопросу о превышении или не превышении скорости света!

Следуя приведенной выше трактовке, во многих научных и научно-популярных статьях слово в слово повторяются эти рассуждения, например, вот что написано в статье [2]:

“Следует, однако, заметить, что условие Vгр > с является чисто формальным, так как понятие групповой скорости введено для случая малой (нормальной) дисперсии, для прозрачных сред, когда группа волн при распространении почти (что такое, почти? Г. И.) не меняет своей формы. В областях же аномальной дисперсии световой импульс быстро деформируется и понятие групповой скорости теряет смысл (это почему теряет? Г. И.); в этом случае вводятся понятия скорости сигнала и скорости распространения энергии (это что, как то связано с вектором Пойнтинга? Г. И.), которые в прозрачных (? Г. И.) средах совпадают с групповой скоростью (? Г. И.), а в средах с поглощением (позрачные среды что, не поглощают, что ли? Г. И.) остаются меньше скорости света в вакууме (это почему?! Г. И.)”.

Вот такие “объяснения” можно прочитать! Если в книге [1] скромно упоминается некое “специальное исследование”, то в последующих “объяснениях” забывают даже и это!

Дальше – больше!

В настоящее время исследован ряд сред, в которых возможно распостранение электромагнитной волны со скоростью, превышающей скорость света в вакууме [3]. В некоторых средах оно распостраняется даже без искажения импульса. Кроме того, эксперименты показали наличие сверхсветовых скоростей и в вакууме (волновод, ближняя зона антенны). Для релятивистов наступили трудные времена, но народ они изобретательный и вот один из “доводов”, приведенный в научно-популярной статье, взятой из того же сайта [2] с интересным названием (впрочем, эта статья кочует из сайта в сайт):

“Дело в том, что, как известно из классических учебников по электродинамике, истинная скорость распространения сигнала — это скорость самого переднего фронта импульса, так называемого предвестника. Можно сказать, что предвестник — это та точка (фронт), где мощность светового импульса отрывается от тождественного нуля. В классической электродинамике показывается, что независимо от свойств среды скорость распространения предвестника всегда равна с”. Интересно, в какой это “классической электродинамике” сказано это? И что это за “предвестник”? И представьте себе картинну, когда передний фронт отстает от несущей волны? Шарлатанство, однако!

Рекомендуем скачать другие рефераты по теме: новшество, реферати українською.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата