Claw.ru | Рефераты по науке и технике | Геометрическая теория строения материи Геометрическая теория строения материи | Категория реферата: Рефераты по науке и технике | Теги реферата: сочинение рассказ, англия реферат | Добавил(а) на сайт: Переверзев. Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата	-6	12	20 - ( 8 -6+12) = - 6
Ребра	30	12	-12	30	30 - (12-12+30) = 0

При этом появляется шесть новых граней, а шесть вершин пропадают. Логично предположить, что при распаде мюона, шесть вершин развернулись в шесть граней. При этом Мюонное нейтрино сохранило оси симметрии Мюона, Электрон получил электрический заряд, а появившиеся оси симметрии Электрона компенсируют оси симметрии Электронного антинейтрино.

Отдельно стоит отметить то, что представление электрона в виде куба объясняет строение молекул. Если куб представить в виде вектора, проходящего из одной вершины в другую через центр, то количество возможных положений вектора в трехмерном пространстве будет равно восьми. Следовательно, электрон может находиться в определенной области пространства в восьми возможных положениях, что равно максимальному количеству электронов в общих валентных оболочках атомов, связанных в молекулу.

Конечно, в Табл. 2 отсутствуют еще два Лептона: это Тау –лептон, и его нейтрино. Поскольку первый лептон – Электрон, состоит из граней с четырьмя сторонами, второй лептон – Мюон, из граней с пятью сторонами то, многогранник Тау-лептона должен состоять из правильных шестиугольников, а Тау-нейтрино, соответственно из правильных треугольников, причем оба многогранника должны быть дуальны..

Но других правильных выпуклых многогранников больше нет. Да, и составить многогранник, состоящий только из правильных шестиугольников невозможно. Видимо, следует обратить внимание на иные многогранники, а именно выпуклые Параллелоэдры (Тела Федорова). И среди них мы заметим Гексагон, многогранник, представляющий собой прямую призму с правильным шестиугольником в основании, и высотой, равной, стороне шестиугольника и дуальный ему Додекатетр, похожий на Октаэдр, только граней у вершины шесть и грани представляют собой равнобедренные треугольники с основанием равным √3/2 от длины боковой стороны.

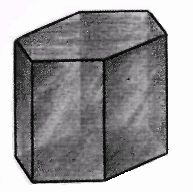
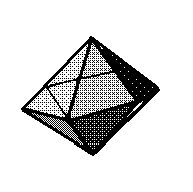
Рисунок 2. Гексагон и Додекатетр

Если Гексагон – Тау-мезон, то Додекатетр – Тау-нейтрино. Объем Гексагона со стороной равной а определим как:

V τ = √3*3/2*а3 (6)

При стороне а = 11 получим :

V τ =3 458,04. (7)

Если сравнить полученную величину с общепринятой величиной массы Тау-мезона (в электронных массах) равной 3 477,50 то увидим, что погрешность определения массы в данном случае менее шести десятых процента, что также не может объясняться простым совпадением.

Логично предположить, что поскольку правильные многогранники исчерпаны, то другие элементарные частицы представляют собой иные многогранники.

Следующими рассмотрим полуправильные многогранники, представляющие собой правильные многогранники, симметрично усеченные.

Первым на такую операцию усечения объема рассмотрим тетраэдр.

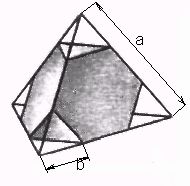
Рисунок 3. Усеченный Тетраэдр

Рекомендуем скачать другие рефераты по теме: шпоры по математике, доклади по биологии.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата