Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

В настоящее время наблюдается ярко выраженная тенденция, направленная на решение определенных физических задач с применением геометрических подходов. Эти подходы нашли широкое распространение в связи с тем, что благодаря им, можно по-новому взглянуть на ряд проблем существующих в некоторых областях физики. Не стало исключением и данное исследование, суть которого сводится к тому, чтобы используя методику естественных геометрических преобразований получить ясную картину для понимания механизма замедления Времени.

В том случае, если мы получим практически точное совпадение показаний координатного Времени, и t при фиксированной координате r , определенной скорости v и при заданном значении соответственно, то в полной мере можно говорить о том, что с физической точке зрения внутренний механизм замедления Времени имеет под собой единую основу.

3.1. Результаты таблицы 1.

Как проводился расчет? Сначала, по формулам (4) и ( 5) устанавливались взаимооднозначные соответствия между текущими значениями фазового угла Времени и конкретными величинами скорости v и координаты r. Другими словами, каждой угловой характеристике находится точное значение v и r . Зная параметры v , r и не трудно найти, и t. Из таблиц видно, в какой степени имеет место согласование показаний Времени для трех случаев.

Ниже, отметим следующие интересные закономерности.

В специальной теории относительности по мере того, как скорость v устремляется к скорости света, где с = 2,997924562х1010 см/сек [2], будет наблюдаться нарастание незначительных отклонений в показаниях часов t и, в первом знаке после запятой. Например, при v = 0,9998476 с , что составляет 99,984759% скорости света и при = 89¦ часы соответственно будут показывать Время = 572,78689 и t = 572,96739 . Мы видим, что эти результаты одинаковые в целой части.

В общей теории относительности при приближении г к, например, г = 1,0003045 и при = 89¦ будет наблюдаться локальная несогласованность в целой части параметров Времени t и, т.е. = 573,06918 и t=572,96739. Однако, используя математические правила округления десятичных дробей не трудно увидеть, что для исходного случая часы будут отсчитывать практически одинаковое Время () . Правда, при =87¦ и = 88¦ имеем, соответсвенно, = 192,10561; t = 191,07306 и = 296,2919 ; t = 286,53295 фиксируется небольшой разброс в показаниях Времени в целой части t и. Какое можно дать объяснение появлению подобного рода аномалий? Можно предположить, что когда значение координаты r становится сравнимым с гравитационным радиусом, то напряженность гравитационного поля возрастает на столько, что активно начинают сказываться топологические флюктуации. Время, да и пространство, в области с высокой кривизной находится в таком физическом состоянии, что становится весьма проблематично указать точные координаты. Так же, при выше указанных значениях фазового угла Времени, возможно происходят процессы, которые не известны физике, на сегодняший день.

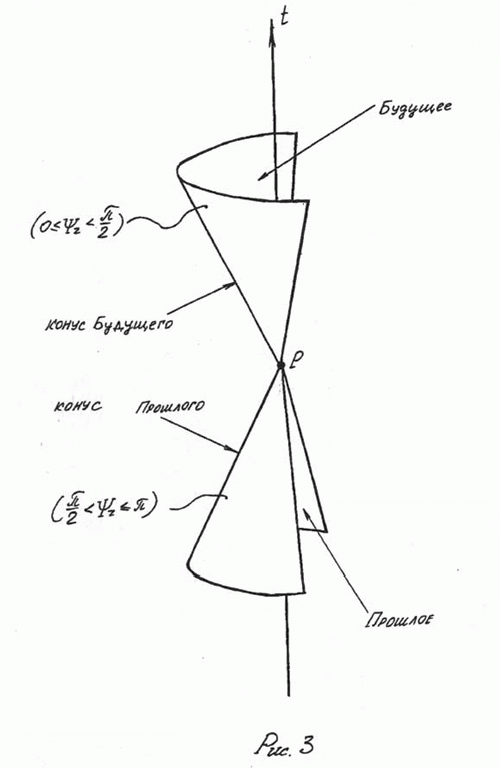
Необходимо сделать следующее замечание. С большой долей вероятности, можно говорить о том, что область изменения фазового угла Времени от 0 до проецируется на световой конус Будущего некоторого события р (Рис.3 ). Схема на Рис.3 с небольшим дополнением заимствована из [1] . Выше представленная позиция справедлива, как для специальной, так и для общей теории относительности. Хотя, в ОТО имеется один нюанс, который выражается в том, что метрика g , задающая световой конус, вообще-то, меняется от точки к точке. Подобная ситуация приводит к несовпадению, в ряде случаев, пространства-времени и топологии евклидового пространства R4 [1]. В данном анализе мы рассматриваем пространство-время без замкнутых времениподобных кривых, т.е. отсутствует нарушение причинности.

Приведенные табличные значения для фазового угла Времени; , лежащего в пределах от 0 до, свидетельствуют о том, что процесс замедления Времени в СТО и ОТО есть унитарное явление и внутренний механизм замедления Времени универсален для обоих эйнштейновских теорий.

3.2. Результаты таблицы 2

Данные полученные в таблице 2 весьма интересны.

По аналогии с разделом 3.1, зная текущее значение, находим v и r . Следующим шагом определяем, и t. В таблице наглядно демонстрируется степень реальной корреляции найденных характеристик.

Из данной таблице выделим две строки, где наблюдается частичное не совпадение в целой части параметров, и t. Укажем их:

1) при = 91¦, что соответствует скорости v = - 0,999847 с и координате г =1,0000859 rg Время измеренное на часах равно tcro = 572,78689;

toTo= 1078,9581 и t =-573,00022;

2) при Tz = 93¦, скорость v = - 0,9986294 с и координате г =1,002717Время оценивается, как = 191,06138; = 192,10561 и t =191,07306. В первом случае расхождения составляют между: a) и; б) и; в) и. Во втором случае имеет место незначительное расхождение, так:

a) и; б) и; в) и. Естественно, что для простоты рассуждений t берется по модулю. Для объяснения полученных аномалий используем гипотезу предложенную при обсуждении результатов таблицы 1 .

Переходя к главному, хочется акцентировать внимание на таких положениях.

В условиях, когда фазовый угол Времени изменяется от 90¦ до 180¦ , скорость v становится, с одной стороны, отрицательной величиной, а с другой - скорость v , взятая по модулю, не превышает по величине скорость света, | v | < с .В контексте сказанного, разумно предложить общеизвестные гипотезы, в связи с доминированием у v знака минус. Первая - координатная система К' переходит в режим равнозамедленного движения (замедление представляет собой отрицательное ускорение) относительно инерциальной системы отсчета К . Вторая - отрицательная скорость возникает в том случае, если будет превалировать движение инерциальной системы отсчета К относительно координатной системы К'. Третья - с физической точки зрения очевидно, что отрицательная скорость, как кинематический критерий, интерпретируется в областях принадлежащих Прошлому.

Хорошо видно, что координата r (расстояние от гравитационного радиуса) в полной мере зависит от. По мере изменения фазового угла Времени от до расстояние от равномерно увеличивается, , переходя при в бесконечность. То есть, полностью исключается ситуация, когда r может стать меньше, чем.

Особенно хочется выделить такой момент. Расчеты показывают, что Время t, отсчитываемое по часам связанными с действием функции секанс фазового угла Времени в границах, образовало группу действительных отрицательных чисел. Легко заметить, что мы получили хорошо известную в физике математическую операцию - операцию обращения Времени, т.е.. Причем, в данном случае, инверсия Времени происходит не "искусственным" путем, а в результате строгих математических действий.

С физической точки зрения, полученная выше процедура априори адекватна тем следствиям, вытекающим из операции обращения Времени, которые известны в физике. Главное - это выполнение условия сохранения определенной симметрии, а так же ряда других условий [3].

И так главное, что хотелось бы выделить. Мы специально приводим данные для и в таблице 2 . Это необходимо для того, чтобы в полной мере показать ситуацию, когда числовые значения и на промежутке, с достаточной степенью точности, эквивалентны и при. То есть, они образовали группу действительных положительных чисел. А это значит, что выражения (1)и(2)не могут дать нам ясной физической картины. Ибо, область изменения от до, явно проецируется на внутренность светового конуса Прошлого некоторого события р (Рис. 3). Что же касается соотношения ( 3 ), то оно без каких-либо затруднений описывает реальные физические условия в области Прошлого.

Отдельно стоит вопрос об экспликации точки. В наших рассуждениях эта точка не входит в промежутки, т.е. она вырезана. Из расчетов видно, что реально можно экстраполировать, возможно, в качестве сингулярной области.

Рекомендуем скачать другие рефераты по теме: ответ 2, мировая экономика.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата