Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

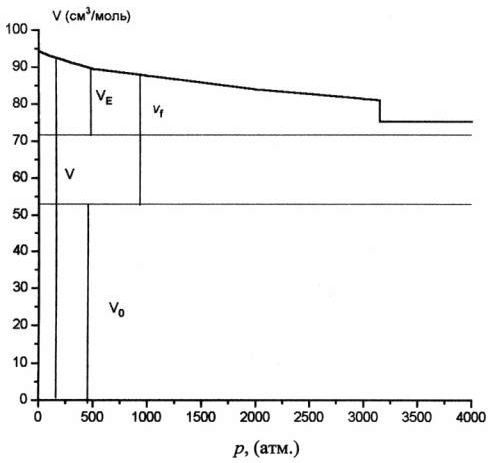
При р=1 атм. vf= 41 см3/моль, a VE =18,4 см3/моль. При р=3125 атм. чистый бензол затвердевает со скачкообразным уменьшением объема на DVs,l =5,7 см3/моль [15]. Эта величина составляет при р = 1 атм. 6% от V(1), 14% от vfи 32% от VE.

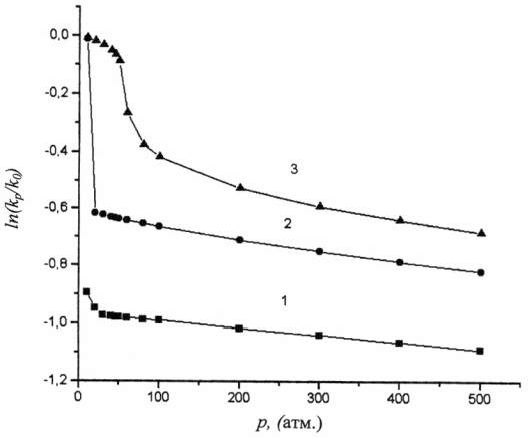 Из рис.3 видно, что зависимостьот p, построенная с использованием VE, намного круче, чем для кривой, построенной с использованием vf. Объем активации, вычисленный по уравнению (1), равен 30,3 см3/моль для первой кривой и только 7,2 см3/моль для второй кривой. Особенно различно их поведение в области затвердевания бензола. Если у второй кривой величина скачканезначительна и лежит в пределах точности кинетических экспериментов, то на первой кривой величина торможения при переходе от жидкого состояния к твердому, так называемый ТЭР = 665. Это чрезвычайно высокое значение. Согласно [15], такой ТЭР могут иметь вещества с температурой плавления tm порядка 2000С. Для бензола, имеющего при атмосферном давлении tm= 5,5530С [14], ТЭР должен быть порядка 1. Более того, в экспериментах над реакциями в растворах не наблюдались скачки скорости при затвердевании растворителя под действием давления, хотя следует заметить, что специально такие эксперименты не ставились. В настоящий момент представляется, что использование vf в уравнении (2) более обосновано, чем использование VE.

Для сравнения результатов, полученных по уравнению (1) и (2) обозначим объем активации в уравнении (1) как, а в уравнении (2) как. Эти объемы активации при р®1атм. относятся как

,

где V(0) и– соответственно, мольный объем и сжимаемость при р®1атм. Величина может быть рассчитана, например, по методу Рао [16,17], групповые инкременты, необходимые для этих расчетов, содержатся в [18]. Таким образом, расчеты по теории Эванса-Поляни дают для объемов активации в растворах величины, в 2 ? 6 раз меньшие, чем дает теория свободного объема.

В настоящее время отсутствуют надежные экспериментальные данные по величинам начальных, мономолекулярных стадий реакций в твердых органических веществах в широком интервале давлений, достаточном для определения влияния давления на константу скорости начальной, мономолекулярной стадии реакции. В экспериментах по влиянию высокого давления на процессы теплового воспламенения или на зажигание ВВ исследуются глубокие, автокаталитические стадии химического процесса, и потому вычисленные в этих работах не относятся к начальным, мономолекулярным стадиям. Однако существует интересное явление, состоящее в резком снижении скорости мономолекулярных реакций в органических веществах при переходе от жидкого состояния к твердому [3,19-21]. Для ряда веществ ТЭР может превосходить 10000. Известно, что при переходе вещества из одной кристаллической модификации в другую скорость химической реакции в нем изменяется. Эти явления могут быть описаны в рамках предлагаемой модели.

При переходе от жидкого состояния к твердому, объем вещества уменьшается примерно на 10% [22]. Это приводит к уменьшению свободного объема и, соответственно, скорости реакции. Величина тормозящего эффекта решетки (ТЭР = для разных веществ лежит в широком интервале от единиц до 104 [17]. Следует учитывать, что при ТЭР >103 реакция локализуется на неравновесных дефектах, дислокациях, границах зерен, поверхности, примесях, и потому истинный ТЭР может быть значительно выше.

Для кристаллических веществ данное выше определение vf нуждается в уточнении. В рамках ячеечной модели Ленард-Джонса [23] свободный объем может быть рассчитан методом атом-атом потенциала [24]. Величину VEможно оценить по тепловому расширению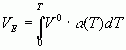, где V0- мольный объем при 0 К, a (Т) - термический коэффициент расширения. Если a = const, то при V0 = 100 см3/моль и Т = 500 K VE равен 5 см3/моль при a= 10-4град-1 и 50 см3/моль при a= 10-3 град-1. Энергоемкие соединения, состоящие из полярных молекул, имеют a= (1 - 2,5).10-4 град-1, величина a» 10-3 град-1 характерны для парафинов [25]. В органических кристаллах от 20 до 36% вещества приходится на пустоты упаковки [25], т.е. на VV. Этот объем не является абсолютно недоступным. По-видимому, при удачном расположении реакционного центра относительно пустот упаковки, они могут быть использованы для создания Vc [21].

Объем активации в кристалле зависит от локального молекулярного окружения и может значительно отличаться от DV?, определенного в растворе, то есть Vc == g. Появление g > 1 можно пояснить на простом примере. Пусть молекула имеет форму шара и Vo =4/3pR3 , а объем активации в виде полусферы с радиусом r?, равный= 2/3 p ( r? )3, расположен в точке касания молекул. Тогда будет иметь форму цилиндра с радиусом R и высотой r? и g= 3/2(V0/2?)2/3. Для DV?= 1; 5 и 10 см3/моль значения и g будут соответственно 33,6; 57,5 и 72,5 см3/моль и 33,6; 11,5; 7,25. В случае, если реакционный центр расположен так, что для образования АК могут быть использованы пустоты упаковки, то g может быть меньше 1. Примером такого соединения может служить 1,3-дифенилтриазен [26].

Пока не выяснено, можно ли применять уравнение (2) для кристаллов. Доводом в пользу его применимости может быть то, что аксиомы ячеечной модели более соответствуют кристаллам, а не жидкостям и газам, для которых она была первоначально предложена, и в рамках которой было введено понятие ”свободный объем” [24].

Если предлагаемая модель справедлива для молекулярных кристаллов, то для веществ, имеющих ТЭР = 104, отношение должно быть 9,2 а для ТЭР = 10=2,3. Несмотря на то, что в рассматриваемой модели свободный объем образует Vс без затрат или выигрыша энергии, чисто комбинаторно, тем не менее дополнительная энергия активациипоявляется из-за температурной зависимости vf.

В [27] было показано, что 1,3,5,7-тетранитро - 1,3,5,7 - тетраазациклооктан в различных полиморфных модификациях имеет различные скорости термораспада. Приняв коэффициент термического расширения для всех трех модификаций равным a= 1,4.10-4 град-1 , получим оценки величин VT и DVs?(см. табл.).

В заключение рассмотрим влияние высокого давления на реакции с отрицательным объемом активации. Примером таких реакций могут служить реакции с циклическим АК. Поскольку характерные времена внутримолекулярных перегруппировок много меньше времен межмолекулярных движений, то химическая реакция происходит при неподвижном молекулярном окружении и потому влияние давления реализуется до начала молекулярной перегруппировки и состоит в упругой деформации молекулы по координате реакции. В результате энергия основного состояния молекулы увеличивается на величину, пропорциональную квадрату давления, соответственно на эту величину уменьшается энергия активации, что приводит к ускорению химической реакции. Так как молекулярное окружение одновременно тормозит внутримолекулярные движения по рассмотренному выше механизму, то суммарное влияние давления можно описать как, где с> 0 - коэффициент, характерный для данной реакции. Так как первый член зависит от давления почти линейно, то зависимость может быть приближенно представлена в виде

.

Следует заметить, что отсутствие внимания к влиянию на скорость реакции плотности вещества и акцентирование внимания на эффектах давления следует, видимо, из того, что при изменении давления в широком диапазоне от атмосферного до тысяч атмосфер плотность меняется незначительно, на несколько процентов.

Список литературы

1. Evans M.G., Polanyi M.//Trans. Faraday Soc. 1935. V.31. P. 875.

2. Van,t Hoff J.H. Lectures on Theoretical and Physical Chemistry. Braunschweig, 1901.

3. Манелис Г.Б. Некоторые особенности механизма реакций в твердой фазе// Проблемы кинетики элементарных химических реакций. М.: Наука. 1973.С.93.

4. Eckert C.A. Annual Review of Physical Chemistry, H.Eyring - Editor for University of Utah. 1972. V. 23. P. 239.

5. Ландау Л.Д., Лифшиц Е.М. Статистическая физика//Теоретическая физика. Т.5. С.56.

6. Бурштейн А.И. Молекулярная физика. Новосибирск: Наука. Сиб. отд- ние, 1986. C 128.

7. Cohen M.H., Turnbull D.// J. Chem. Phys. 1959 V. 31. P. 1164.

8. Глесстон С., Лейдлер К., Эйринг Г. Теория абсолютных скоростей реакций, ИЛ, М., 1948. [Glasstone S., Laidler K., Eyring H. The Theory of Rate Processes. NY and London. Frick Chemical Laboratory. Princeton University. 1941].

9. Asped J.// J. Am. Chem. Soc. 1969. V.91. P. 7580.

Рекомендуем скачать другие рефераты по теме: оформление доклада, курсовая работа производство.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата