Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

и их меры

              Предположим, что  как функция  при фиксированном  непрерывна и строго возрастает. Введем функцию

              Это - монотонное преобразование расстояния, а потому  - метрика или симметрика (т. е. неравенство треугольника может быть не выполнено), которую, как и , можно рассматривать как меру близости между  и .

              Введем

.

              Поскольку  определена однозначно, то

^

где ., а потому

              Переход от  к  напоминает классическое преобразование, использованное Н. В. Смирновым, , переводящее случайную величину  с непрерывной функцией распределения  в случайную величину , равномерно распределенную на [ 0, 1]. Оба рассматриваемых преобразования существенно упрощают дальнейшие рассмотрения.

              Преобразование  зависит от точки , что не влияет на дальнейшие рассуждения, поскольку ограничиваемся изучением сходимости в точке.

              Функцию , для которой мера шара радиуса  равна , называют [4] естественным показателем различия или естественной метрикой. В случае пространства  и евклидовой метрики  имеем

где -объем шара единичного радиуса в .

              Поскольку можно записать, что

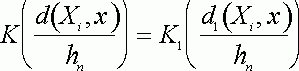
где

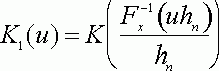
то переход от  к  соответствует переходу от  к . Выгода от такого перехода заключается в том, что утверждения приобретают более простую формулировку.

              ТЕОРЕМА 1. Пусть  - естественная метрика,

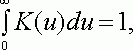
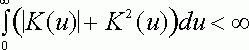
Плотность  непрерывна в  и ограничена на , причем . Тогда , оценка  является состоятельной, т. е. по вероятности при ,

Рекомендуем скачать другие рефераты по теме: доклад по обж, реферат германия.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата