Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Рис.2.

Когда скорость очень мала или вязкость очень велика, можно отбросить инерционные члены и описать поток уравнением

где W - векторное поле,

Это уравнение впервые было решено Стоксом. Он так же решил задачу для сферы. Когда маленькая сфера движется при малых числах Рейнольдса (понятие числа Рейнольдса введено на странице 5), то к ней приложена сила, равная 6ph аV, где а – радиус сферы, V – его скорость. В области малых чисел Рейнольдса линии вокруг цилиндра выглядят так же, как на рисунке 2.

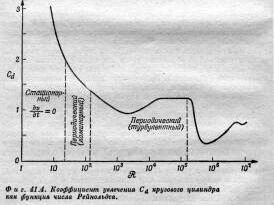
Качественной характеристикой, описывающей поток реальной жидкости, является сила, увлекающая цилиндр. На рисунке 3 графически изображена зависимость коэффициента увлечения Сd, отношения силы к 1/2rV2Dl (D – диаметр, l – длина цилиндра, r - плотность жидкости).

Воздействие статического давления на твердые тела, находящиеся в поле течения

Рисунок рис.4 показывает обтекаемый плоский диск в трёх положениях. Первое оказывается неустойчивым: диск устанавливается поперек течения. Мы видим пример этому на каждом падающем листе бумаги. Объяснение: при любом ничтожном наклонении возникает несимметричность в распределении статического давления, вследствие чего развивается вращательный момент. Это очевидно, когда диск находится под большим наклоном к течению (рис.4,б): области сгущенных линий тока тянут, а области расходящихся линий тока давят против диска, т.е. в ту же сторону. В результате, диск поворачивается по часовой стрелке (рис.4,б).

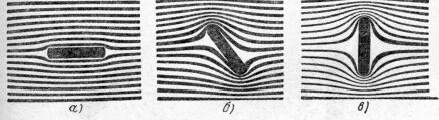
Рис. 4.

 

Вязкий поток

В общем случае сжимаемой жидкости в напряжениях есть и другой член, который зависит от производных скорости. Общее выражение имеет вид

Где dij обозначает символ Кронекера, который равен единице при i=j и нулю при i?j). Ко всем диагональным элементам S тензора напряжений прибавляется дополнительный член . Если жидкость несжимаема, торавно нулю и дополнительного члена не появляется, так как он действительно имеет отношение к внутренним силам при сжатии. Коэффициент h - коэффициент вязкости.

Число Рейнольдса

Если мы решили задачу для потока с одной скоростью V1 и некоторого цилиндра диаметром D1 а затем интересуемся обтеканием другого цилиндра диаметра D2 другой жидкостью, то поток будет одним и тем же при такой скорости V2, которая отвечает тому же самому числу Рейнольдса, которое выражается зависимостью

VD

Это соответствует действительности только в том условии, что сжимаемостью жидкости можно пренебречь. В противном случае модели будут соответствовать, если будут одинаковы одновременно число Рейнольдса и число Маха (число Маха - отношение V к скорости звука). Таким образом, для скоростей, близких к скорости звука и больших, поток в обоих случаях будет одинаков, если и число Маха и число Рейнольдса равны.

Если увеличивать скорость потока так, что число Рейнольдса станет несколько больше единицы, то увидим, что поток изменился. За сферой возникают вихри (см рис. 5). Обычно считают, что циркуляция нарастает постепенно. Когда ? =от 10 до 30 поток меняет свой характер.

Когда число Рейнольдса проходит значение в районе 40, характер движения претерпевает неожиданное и резкое изменение. Один из вихрей за цилиндром становится настолько длинным, что отрывается и плывет вниз по течению вместе с жидкостью. При этом жидкость за цилиндром снова закручивается и возникает новый вихрь. Вихри отслаиваются то с одной, то с другой стороны и в какой-то момент вытягиваются вихревым следом за цилиндром. Такой поток вихрей называется цепочкой Кармана. Она всегда появляется для чисел Рейнольдса ?>40.

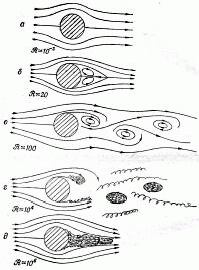
Рис. 5.

 

Можно представить физическую причину этих вихрей. Известно, что на поверхности цилиндра скорость жидкости должна быть равной нулю, но при удалении от поверхности скорость быстро возрастает. Это местное изменение скорости жидкости и создаёт вихри. Если скорость достаточно мала, у вихрей есть время “расплыться” на большую область. Когда ?достигает нескольких тысяч, вихри начинают заполнять тонкую ленту. В таком слое поток хаотичен и нерегулярен. Эта область называется пограничным слоем . Этот поток пробивает себе дорогу дальше и дальше. В этой области, турбулентности, скорости очень нерегулярны и беспорядочны. С увеличением числа Рейнольдса до 105, мы получаем турбулентный след.

Всплывающий воздушный пузырек и закон Архимеда.

Когда пузырек всплывает, некоторая масса воды устремляется вниз, заполняя освобожденное место. Пузырек взаимодействует с движущейся, а не с неподвижной водой. Внешне это выглядит так, что c массой всплывающего пузырька движется “присоединенная масса” воды, которая равна ?m=Vr/2,т.е. половине массы вытесненной воды. Это происходит из-за сложного движения жидкости вокруг самого пузырька.

Ламинарные и турбулентные течения в природе и технике

Рекомендуем скачать другие рефераты по теме: шпори для студентів, контрольная 3.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата