Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

1. Вследствие однородности пространства и времени преобразования должны быть линейными.

Действительно, если бы производные функций по не были бы константами, а зависели от то и разности , выражающие проекции расстояний между точками 1 и 2 в "движущейся" системе, зависели бы не только от соответствующих проекций , в "неподвижной" системе, но и от значений самих координат что противоречило бы требованию независимости свойств пространства от выбора начальных точек отсчета. Если положить, что проекции расстояний вида x ' = = зависят только от проекций расстояний в неподвижной системе, т.е. от x = , но не зависит от , то

при т.е. или .

Аналогично можно доказать, что производные по всем другим координатам также равны константам, а следовательно, и вообще все производные по суть константы.

2. Выберем "движущуюся" систему таким образом, чтобы в начальный момент точка, изображающая ее начало координат, т.е. совпадала с точкой, изображающей начало координат "неподвижной" системы, т.е. , а скорость движения системы была бы направлена только по

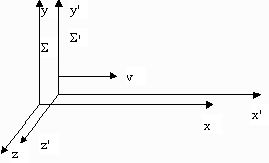Если мы также учтем требование изотропности пространства, то линейные преобразования для системы отсчета , выбранной указанным образом, запишутся в виде Здесь отсутствуют члены, содержащие и в выражениях и , в силу изотропности пространства и наличия единственного выделенного направления вдоль оси , соответственно постановке задачи. На этом же основании в выражениях для и отсутствуют члены, пропорциональные, соответственно, и , а коэффициенты при и одинаковы. Члены, содержащие и , отсутствуют в выражениях для и в силу того, что ось все время совпадает с осью . Последнее было бы невозможно, если бы и зависели от и .

3. Изотропность предполагает также симметричность пространства. В силу же симметрии ничто не должно измениться в формулах преобразования, если изменить знаки и , т.е. одновременно изменить направление оси и направление движения системы . Следовательно, (d) Сравнивая эти уравнения с предыдущими () получаем:

. Вместо удобно ввести другую функцию , так, чтобы выражалось через ипосредством соотношения Согласно этому соотношению, - симметричная функция. Используя это соотношение, преобразования (d) можно записать в виде 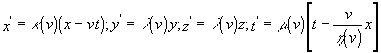(e), причем все входящие в эти формулы коэффициенты суть симметрии функции .

4. В силу принципа относительности обе системы, "движущаяся" и "неподвижная", абсолютно эквивалентны, и поэтому обратные преобразования от системы кдолжны быть тождественно прямым от к. Обратные преобразования должны отличаться лишь знаком скорости , т.к. системадвижется относительно системывправо со скоростью , а система движется относительно системы (если последнюю считать неподвижной), влево со скоростью . Следовательно, обратные преобразования должны иметь вид 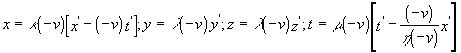. (f) Сравнивая эти преобразования с (e), получаем . Но в силу симметрии получаем, что , т.е. . Очевидно, имеет смысл лишь знак (+), т.к. знак (-) давал бы при перевернутую по и систему. Следовательно . Замечая, что коэффициенты - тоже симметричные функции , первое и последнее уравнение из (e) и (f) можно записать в виде: А) , а) , В) , в) . Умножая А) на , В) на и складывая, получим . 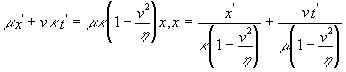Сравнивая это выражение с а), получаем 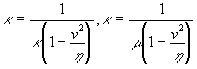. Откуда имеем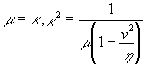

Следовательно, извлекая квадратный корень и замечая, что знак (-) так же, как и для , не имеет смысла, получаем 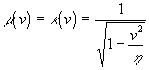. Итак преобразования приобретают вид: 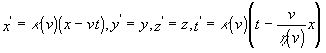(g) или ,подробнее: 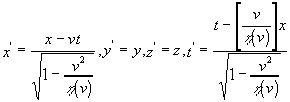,(h) где - неизвестная пока функция .

5. Для определения вида обратимся вновь к принципу относительности. Очевидно, что преобразования (g) должны быть универсальными и применимыми при любых переходах от одних систем к другим. Таким образом, если мы дважды перейдем от системык и от к , то полученные формулы, связывающие координаты и время в системе с координатами и временем в, должны также иметь вид преобразований (g). Это вытекающее из принципа относительности требование, в совокупности с предыдущими требованиями обратимости, симметрии и т.д. означает, что преобразования должны составлять группу.

Воспользуемся этим требованием групповости преобразований. Пусть - скорость системы относительнои - скорость системы относительно системы

Тогда согласно (g)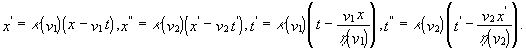

Выражая и через и , получаем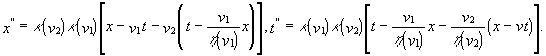

Согласно сформулированному выше требованию эти же преобразования должны записываться в виде (g), т.е. 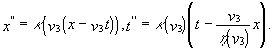(k) Коэффициенты, стоящие при в первой из этих формул и при во второй, одинаковы. Следовательно, в силу тождественности предыдущих формул и этих, должны быть одинаковы и коэффициенты, стоящие при в первой из предыдущих формул и приво второй из формул (h) т.е. 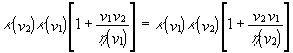. Последнее равенство может быть удовлетворено только при

6. Итак, в преобразованиях (h) h является константой, имеющей размерность квадрата скорости. Величина и даже знак этой константы не могут быть определены без привлечения каких-либо новых допущений, опирающихся на опытные факты.

Если положить , то преобразования (h) превращаются в известные преобразования Галилея Эти преобразования, справедливые в механике малых скоростей (), не могут быть приняты как точные преобразования, справедливые при любых скоростях тел, когда становится заметным изменение массы тел со скоростью. Действительно, учет изменения массы со скоростью приводит к необходимости принять положение об относительности одновременности разобщенных событий. Последнее же несовместимо с преобразованиями Галилея. Таким образом, константа h должна быть выбрана конечной.

Из опыта известно, что при больших скоростях, сравнимых со скоростью света, уравнения механики имеют вид 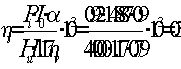(i), где - собственная масса, совпадающая с массой частицы при малых скоростях (), с - константа, имеющая размерность скорости и числено равная см/сек, т.е. совпадающая со скоростью света в пустоте. Этот опытный факт трактуется как зависимость массы от скорости, если массу определить как отношение импульса тела к его скорости.

Константа имеет такую же размерность, какую имеет h , входящая в формулы преобразования координат и времени (h). Естественно поэтому положить (j), поскольку в экспериментально полученную зависимость массы от скорости не входит никакая иная константа, имеющая квадрата скорости. Принимая это равенство, преобразования (h) записываются в виде (l).

Пуанкаре назвал эти преобразования координат и времени преобразованиями Лоренца.

В силу обратимости обратные преобразования Лоренца, очевидно, должны быть записаны в виде

Примененные нами соображения размерности для выбора константы h не вполне, однако, однозначны, т.к. вместо соотношения (j) с таким же правом можно было бы выбрать (k)

Оказывается, однако, что совпадающие с опытом уравнения механики (i) могут быть получены лишь как следствия преобразований Лоренца и не могут быть совмещены с преобразованиями, получающимися из допущения (k). Действительно, известно, что уравнения механики, опирающимися на преобразования Лоренца, являются уравнения Минковского, согласно которым масса увеличивается со скоростью по формуле

. Если же в качестве преобразований координат выбрать , то соответствующие уравнения Минковского дадут убывающую со скоростью массу m, что противоречит опыту.

Итак, не обращаясь к постулату о постоянстве скорости света в пустоте, не ссылаясь на электродинамику и не используя свойств световых сигналов для определения одновременности, мы вывели преобразования Лоренца, используя лишь представление об однородности и изотропности пространства и времени, принцип относительности и формулу зависимости массы от скорости.

Рекомендуем скачать другие рефераты по теме: реферат вода, банк курсовых работ бесплатно.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата