О теоретических положениях динамики и устойчивости бурильной колонны и способах их реализации на практике

| Категория реферата: Рефераты по науке и технике
| Теги реферата: доклад, реферат на тему здоровье
| Добавил(а) на сайт: Kurbatov.

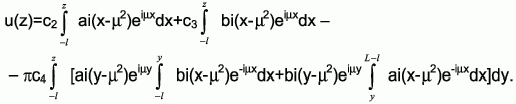 (6)

Для дальнейших вычислений нам понадобятся выражения элемента a13 специального определителя, возникающего в результате подстановки (6) в граничные условия:

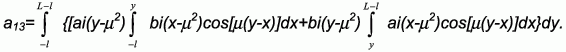
Здесь ai(.) и bi(.)— стандартные специальные функции Эйри [9].

Раскрывая cos[µ(y-x)] по формуле сложения аргументов, пользуясь известной асимптотикой для ai(x) и bi(x) при больших значениях аргумента, нетрудно установить, что a13 ≈ lnL/ при L>>1.

В случае условий шарового шарнира равенство нулю спектрального определителя упрощается к виду:

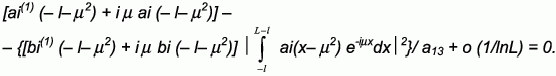 (7)

Поскольку ai(x) и ее производная не обращаются в ноль одновременно в одной и той же точке [9], первое слагаемое (7) не обращается в ноль ни при каких l и µ.

В случае заделки (7) упрощается к виду, в котором отсутствуют ai(1) (— l— µ2) и bi(1) (— l— µ2) , а множитель i µ заменяется на 1 в выражениях в [ ].

В случае полукасательных (по Болотину) условий (7) сводится к отсутствию чисто мнимых слагаемых. Два последних самосопряженных варианта граничных условий приводят к потере устойчивости путем изгиба. При этом действительные значения критических нагрузок слабо (на слагаемое µ2) отличаются от соответствующих значений для плоского случая.

Отсутствие корней уравнения (7) в случае шарнирного опирания означает возможность потери устойчивости бурильной колонны путем развития неуправляемых поперечных колебаний, на которые теряется подводимая к колонне энергия вне зависимости от способа бурения.

Важнейшим результатом наших исследований явилось то, что при использовании ГЗД флаттер колонны может возникнуть из-за реактивного крутящего момента, что не принимали во внимание ни Лейбензон, ни Капелюшников, ни другие авторы.

Для исключения самой возможности флаттера предлагается изменить характер взаимодействия колонны бурильных труб со стенками в соответствии с результатами теоретического изучения не одиночного опорно-центрирующего устройства, а пары ОЦУ.

Обычные ОЦУ обеспечивают непрерывность функции прогиба, ее первой и второй производных (угол наклона и изгибающий момент) и допускают разрыв третьей производной (скачок перерезывающей силы, в нашем случае, реакции со стороны стенки на опору). При рассмотрении нескольких ОЦУ возникает многоточечная разрывная краевая задача, описываемая дифференциальным уравнением изгиба колонны 4-го порядка, приводящаяся к алгебраической системе относительно 4(n+1) произвольных постоянных (n — число ОЦУ). Устойчивые численные методы для решения таких задач предложены в [10-11].

Аналитическое исследование названных задач начинается с представления на каждом участке колонны между ОЦУ общего решения yi дифференциального уравнения, обобщающего дифференциальное уравнение изгиба стержней в виде: индекс i соответствует номеру участка колонны между опорами, {uk}, k=1,2,3,4 — полная система линейно независимых решений однородного дифференциального уравнения упругого изгиба стержней (ДУУИС), f(s)-частное решение неоднородного ДУУИС:

y(4) + a1∙y(3) + a2∙y(2) + a3∙y(1) + a4∙y = 0, (8)

y(4) + a1∙y(3) + a2∙y(2) + a3∙y(1) + a4∙y = (s). (9)

Рассмотрим для уравнения (9) четырехточечную краевую задачу с двумя внутренними граничными условиями в точках s1 и s2, соответствующую в обычном понимании КНБК с двумя полноразмерными центраторами:

y(0)=y(2)(0)=0; y(L)=y(2)(L)=0; 0

Скачали данный реферат: Gurskij, Табаков, Kunaev, Chupalov, Jashin, Avandeev.
Последние просмотренные рефераты на тему: контрольные бесплатно, виды шпор, реферат данные, образ реферат.