Об алгоритмах самоорганизации в задаче синтеза информационных технологий обработки сигналов
| Категория реферата: Рефераты по науке и технике
| Теги реферата: бесплатные дипломные работы скачать, сообщение об открытии счета
| Добавил(а) на сайт: Бабышев.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
Природа
пошла навстречу в разрешении этой проблемы. Дело в том, что в момент начала
кристаллизации происходит экзотермическая реакция - выделения скрытой теплоты
кристаллизации. Поэтому, если зарегистрировать процесс охлаждения расплава (см.
правую часть рис. 6), то на графике процесса 
(термограмме)
при достижении температуры ликвидуса появляется своеобразный фрагмент в виде
температурной остановки (площадки). Обнаружив такой информативный фрагмент
термограммы можно определить температуру 
, а затем и
процентное содержание углерода по модели (4).
Предположим
теперь, что нам известна лишь первая часть описанных выше закономерностей, т.е.
только гипотеза о том, что термограмма несет информацию об интересующем нас
параметре 
, но
неизвестно каким образом. Можно ли в этих условиях воспользоваться идеями
самоорганизации для восстановления зависимости (4) по экспериментальным данным
?
На первый взгляд может показаться, что такую задачу имеет простое решение в классе алгоритмов самоорганизации, но в этом как раз и состоит “вульгаризация” идеи МГУА!
Пусть
в нашем распоряжении имеется выборка термограмм, зарегистрированных для W проб
металла, и для каждой такой пробы на основании результатов химического анализа
известно точное значение содержания углерода C1,…,CW . Будем считать, что
каждая из W термограмм представлена своими дискретными значениями 
.
Поскольку
в векторах 
содержится вся
доступная нам информация о термограмме, то можно считать значения потенциальными
регрессорами, для которых известно точное значение отклика . Другими
словами считать, что в нашем распоряжении имеется выборка, содержащая W точек
наблюдений, образующих 
матрицу
регрессоров и W-мерный вектор отклика (см. таблицу 1).
Казалось бы, имея такую выборку, легко можно восстановить закономерность (4), задав класс базисных функций в виде всевозможными линейных структур
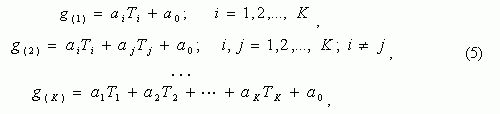
Таблица 1. Гипотетическая выборка наблюдений
|
№ |
Регрессоры (аргументы модели) |
Отклик (выход) |
||||||
|
T1 |
T2 |
T3 |
… |
TK |
||||
|
1 |
T1[1] |
T2 [1] |
T3 [1] |
… |
TK [1] |
C1 Рекомендуем скачать другие рефераты по теме: характеристика реферата, скачать сообщение. Категории:Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
Главная