
Об энтропийной оценке сверхпластичности
| Категория реферата: Рефераты по науке и технике
| Теги реферата: курсовая работа по предприятию, образ сочинение
| Добавил(а) на сайт: Астахов.
1 2 3 | Следующая страница реферата
Об энтропийной оценке сверхпластичности
Я. И. Рудаев, Е. Н. Шестаева
Кыргызско-Российский Славянский Университет, Бишкек
Рассматривается задача соответствия модели сверхпластичности процессу деформации с размытым фазовым переходом. Показано, что в оптимальных термодинамических режимах сверхпластичности минимизируется производство энтропии, которому соответствует формирование равноосной ультрамелкозернистой структуры.
Эффект сверхпластичности металлов и сплавов внешне проявляется в форме аномального квазиоднородного удлинения при малых значениях напряжений пластического течения. Металловедческими исследованиями установлено [1,2], что специфика подобной аномалии заключается в превалировании механизма зернограничного проскальзывания над другими формами массопереноса. Реализации указанного механизма способствует формирование ультрамелкозернистой структуры на предварительном этапе (структурная или микрозеренная сверхпластичность) или в процессе нагрева и деформации (динамическая сверхпластичность). Очевидно, что динамическая сверхпластичность имеет место в промышленных металлических материалах, которые реагируют на изменение температурных и кинематических условий в виде различной природы структурных превращений [3]. В частности, промышленные алюминиевые сплавы в исходном литом и деформированном состояниях проявляют сверхпластические свойства в термомеханических режимах структурного фазового перехода – динамической рекристаллизации [3 … 8]. В процессе последней в материале возникает равновесная структура с очень мелким зерном, примерно совпадающим по размерам с субзернами. Так создается структурная ситуация, способствующая осуществлению зернограничного проскальзывания. Наличие ультрамелкого зерна можно считать необходимым, но недостаточным условием развития эффекта. К микрозернистости следует добавить требование равноосности и несклонности к росту зерна при нагреве и деформации [2]. Важным структурным элементом считаются также границы зерен [9].
Отмеченный факт был использован при формулировке модели [10, 11], адекватно с позиций механики деформируемого твердого тела отражающей накопленные экспериментальные данные. Модель описывает поведение алюминиевых сплавов не только при сверхпластичности, но и в пограничных областях термопластичности и высокотемпературной ползучести.
Естественно оценить модель [10, 11], с точки зрения определения представляющих реальный интерес физических величин и получения дополнительной информации. Очевидно, что динамической сверхпластичности соответствует размытый фазовый переход [12] и поэтому целесообразно проследить за поведением функций отклика, которые сравнительно легко определяются при известном аналитическом выражении плотности термодинамического потенциала. К указанным функциям можно, прежде всего, отнести энтропию.
Исследование функции энтропии позволяет рассматривать процесс деформации с позиций самоорганизации диссипативных структур возрастающей сложности в неравновесных открытых системах [13].
При формулировке модели энергетическая функция состояния была принята в форме термодинамического потенциала Ландау с учетом внешнего поля
![]() . (1)
. (1)
Здесь![]() ;
; ![]() - параметр
порядка;
- параметр
порядка; ![]() - напряжение
пластического течения;
- напряжение
пластического течения; ![]() - скорость
деформации;
- скорость
деформации; ![]() - управляющий
параметр;
- управляющий
параметр; 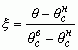 -
нормированная температура;
-
нормированная температура; ![]() - постоянная
материала; причем
- постоянная
материала; причем![]() ,
, ![]() - внутренние
альтернативные параметры состояния;
- внутренние
альтернативные параметры состояния; ![]() - абсолютная
температура;
- абсолютная
температура; ![]() - нижняя и
верхняя границы термического диапазона сверхпластичности.
- нижняя и
верхняя границы термического диапазона сверхпластичности.
Легко видеть аналогию функции (1) с явным выражением
потенциала катастрофы сборки [14]. Очевидно теперь, что если![]() , то изменений
структурного характера в деформируемом материале не происходит. Условие
, то изменений
структурного характера в деформируемом материале не происходит. Условие ![]() соответствует
структурно неустойчивому состоянию среды. Значение
соответствует
структурно неустойчивому состоянию среды. Значение ![]() отвечает
переходным состояниям.
отвечает
переходным состояниям.
На параметр порядка накладываются следующие ограничения
на область структурных превращений
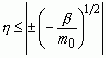 ; (2)
; (2)
на диапазон развития сверхпластичности
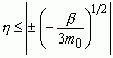 . (3)
. (3)
Кинетическое уравнение для управляющего параметра имеет вид
![]() , (4)
, (4)
где ![]() - скорость
возрастания нормированной температуры,
- скорость
возрастания нормированной температуры, ![]() - функция
чувствительности среды к структурным превращениям, определяемая следующим
образом
- функция
чувствительности среды к структурным превращениям, определяемая следующим
образом
![]() , (5)
, (5)
причем ![]() - степень
полноты развития фазового перехода, равная
- степень
полноты развития фазового перехода, равная
![]() ; (6)
; (6)
![]() - постоянные
материала.
- постоянные
материала.
Для внутренних параметров состояния получены эволюционные уравнения
![]() , (7)
, (7)
Рекомендуем скачать другие рефераты по теме: лес реферат, решебник по русскому.
Категории:
1 2 3 | Следующая страница реферата
 Главная
Главная