Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Однако, после непродолжительных экспериментов стало очевидно, что наиболее хорошее приближение получается, если за основу взять обобщение гиперболы

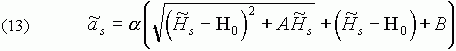
где,, A и B - неизвестные коэффициенты, которые требуется найти.

При этом коэффициентопределяет масштаб и выражается в астрономических единицах,определяет расположение фокуса гиперболы, A - ее кривизну, B - начальное смещение при s=0, поскольку в ходе исследований выяснилось, что не удается добиться хорошей аппроксимации, если зафиксировать значениеравным нулю. Это объясняется тем, что само Солнце за счет своего собственного вращения, ненулевых размеров и возмущений от планет имеет ненулевую скорость хода времени относительно центра Солнечной системы.

Функция (13) является "фильтром", отделяющим идеальную пропорцию ОЗС от реальности. Если такая характеристика как соотношение площадей воды и суши на поверхности Земли оказалась зависящей от ОЗС по линейному закону, то большие полуоси планет оказались гиперболической функцией от ОЗС. Объяснять этот факт можно различными путями, однако близость данной зависимости к гиперболе очевидна и может быть принята за рабочую гипотезу.

В качестве исходных данных для аппроксимации были взяты большие полуоси главных планет на 27 июня 1992 года [5]. Для пояса астероидов (по одной из гипотез здесь была орбита разрушенной планетыФаэтон) была взята большая полуось орбиты астероида Церера [5] и весовой коэффициент 0,5. Для Солнца "период обращения" был приравнен к периоду его собственного вращения (около 25 часов). Решение искалось методом наименьших квадратов и были получены следующие значения коэффициентов:

		622,70482193
		0,8154296084
		0,0004920468
		-0,0003427966

Результаты вычислений по формуле (13) при этих коэффициентах приведены в таблице 3 и на рисунке 3.

Таблица 3

s	Название	, а.е.	,год идеальный цикл	, а.е.	, год реальный цикл	, %
0	Солнце	0,0292323	0,0049980	[0,0201477]	[0,0028520]	[-36,79]
1	Меркурий	0,2652667	0,1366231 ~50 дней	0,3870972	0,2408408 ~88 суток	37,35
2	Венера	0,5682112	0,4283164 ~156 суток	0,7233286	0,6151817 ~225 суток	24,02
3	Земля	0,9941917	0,9913002 ~362 дня	0,9999846	0,9999769 ~365 дней	0,58
4	Марс	1,6503591	2,1201553	1,5236959	1,8808209	-7,98
5	Фаэтон	2,7855127	4,6489803	[2,7688824]	[4,6074090]	[-0,60]
6	Юпитер	5,0640356	11,395808	5,2031024	11,868438	2,71
7	Сатурн	10,099045	32,093748	9,5219707	29,382603	-5,88
8	Уран	19,014111	82,911361	19,201051	84,137093	0,98
9	Нептун	29,602015	161,05785	30,073664	164,92235	1,58
10	Плутон	39,881622	251,86001	39,724908	250,37695	-0,39
11	Сома	49,302596	346,18216
12	Дхарма	57,818584	439,64402
13	Род	65,507058	530,19075
14	Тот	72,467239	616,89688
15	Аредвисура	78,793033	699,40983
16	Митра	84,566649	777,67597
17		89,858233	851,79838
18		94,727183	921,95969
19		99,223783	988,37936
20		103,39073	1051,2896
21		107,26442	1110,9219
22		110,87607	1167,4996
23		114,25255	1221,2338

Значениепредставляют собой относительное различие между вычисленными (идеальными)и реальнымизначениями больших полуосей:

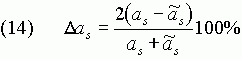
Наибольшие отклоненияполучились для Солнца, Меркурия и Венеры, то есть для тел, расположенных в непосредственной близости к центру системы. По видимому, это объясняется тем, что Солнце, являясь генератором времени, искривляет время вокруг себя, что особенно заметно на малом расстоянии. Погрешности для остальных планет являются доказательством того, что они находится не точно на устойчивых орбитах, а в их окрестности.

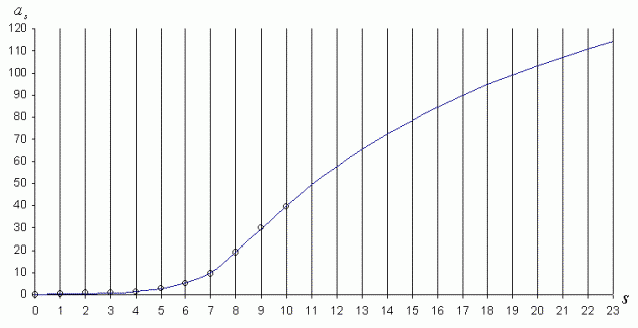
рис. 3

Из таблицы 3 и рисунка 3 видно, что, если гипотеза о связи ОЗС со значениями больших полуосей верна, за Плутоном должны существовать планеты с циклами около 346, 440, 530, 617, 699, 777 и так далее лет. Конечно, не на всех устойчивых орбитах обязательно существуют планеты, но опыт с Фаэтоном показывает, что свято место пусто не бывает и даже если там нет одной большой планеты, там должно находиться эквивалентное по массе количество малых тел. Автор взял на себя риск, исходя из мифологии, предложить имя одной из дальних (высших) планет. Кроме того, опираясь на некоторые данные, почерпнутые из древних текстов, можно предположить, что эклиптическая долгота планеты с циклом 440 лет, которую предлагается назвать Дхарма (в буддизмеДхарма - это общий универсальный мистериальный принцип взаимосвязи всех законов и явлений в мироздании, закон перемен, причинно-следственных изменений, универсальный вселенский закон причин и следствий), на середину 1996 года составляет примерно 43 градуса.

Обратим внимание, что фокус гиперболы лежит между значениями s=7 и s=8, то есть между Сатурном и Ураном, как раз на грани между планетами, видимыми невооруженным глазом, и планетами дальними, открытыми лишь относительно недавно. Кроме того, вблизи этой точки перегиба находится замечательный астероид Хирон (2060), который больше похож на планетоид, чем на осколок разрушенного небесного тела, как большинство других астероидов. Еще более интересно, что самая большая планета Солнечной системы - Юпитер, который иногда называют несостоявшейся звездой - попала почти точно в точку перегиба гиперболы (рис.2)! Не потому ли Юпитер "набрал" самый большой вес, что его орбита находится как раз на этом перегибе?

Из (13) также следует, чтоа.е.,

Следующим этапом нашего анализа будет рассмотрение систем спутников планет, имеющее своей целью подтвердить или опровергнуть гипотезу о связи ОЗС с большими полуосями через функцию (13).

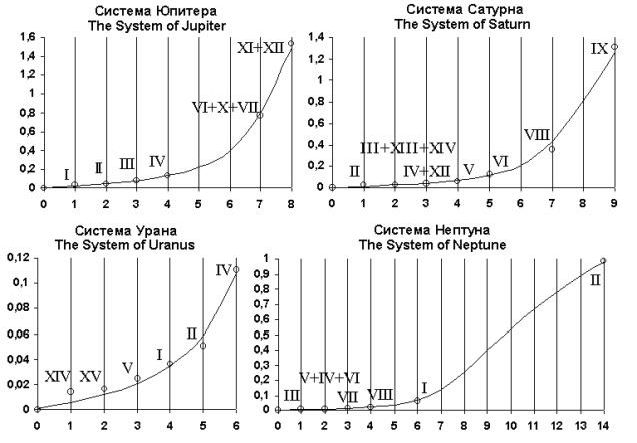
рис. 4

Наибольший интерес представляют системы спутников Юпитера, Сатурна, Урана и Нептуна. Скажем несколько слов о том, как проводился анализ. В первую очередь из рассмотрения пришлось исключить часть тел, имеющих неправильную форму, так как в большинстве своем они явно не укладывались ни в какую гладкую аппроксимацию. Также пришлось исключить из рассмотрения несколько весьма незначительных по размерам ближайших спутников в системах Юпитера, Сатурна и Урана. Предварительный анализ показал, что все системы спутников планет Солнечной системы хорошо аппроксимируются зависимостью (13), умноженной на поправочный коэффициентуникальный для каждой конкретной системы. Результаты этой аппроксимации для систем спутников Юпитера, Сатурна, Урана и Нептуна приведены на рисунке 4 (по оси абсцисс отложены значения s, по оси ординат - значения). Значения поправочных коэффициентовданы в таблице 4 и в виде графика на рисунке 5.

Приведенные на рисунке 4 графики позволяют сделать заключение, что общий вид и даже все параметры формулы (13) остаются практически без изменений в пределах всей Солнечной системы.

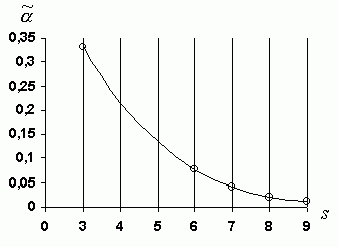
рис. 5

Таблица 4

s	Планета
3	Земля	0,3315
6	Юпитер	0,0783
7	Сатурн	0,0428
8	Уран	0,0212
9	Нептун	0,0135

Из рисунка 5 и данных таблицы 4 очевидно, что коэффициентзависитобратно пропорционально от большой полуоси:

То есть чем дальше от Солнца находится система, тем более она "сжата", тем стремительнее уменьшаются большие полуоси устойчивых орбит спутников при тех же значениях s. Противоположная картина наблюдается при приближении к Солнцу: здесь устойчивые орбиты спутников стремительно "раздуваются" и поэтому, к примеру, у Меркурия вообще не может быть спутников, так как первая ближайшая к нему устойчивая орбита спутника настолько велика, что любое тело, помещенное на нее, либо упадет на Солнце, либо переместиться на околосолнечную орбиту и станет еще одной малой планетой.

Отдельного рассмотрения заслуживает система спутников нашей с вами планеты - Земли. Коэффициент=0,3315 был выбран исключительно из того предположения, что идеальный цикл Луны должен составлять около 30 земных суток и Луна находится на орбите вокруг Земли соответствующей ОЗС при s=2.

Рекомендуем скачать другие рефераты по теме: бесплатные тесты, курсовая работа по организации.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата