Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Первым, кто указал на прямую связь между хаосом и потоками жидкости, был советский математик В.И. Арнольд. В 1965 г. Арнольд предположил, что в жидкостно-механических системах траектории частиц могут быть хаотическими. Французский астроном из Обсерватории в Ницце М. Эно развил идею Арнольда и в статье объемом всего три страницы с одним рисунком смог показать, что стационарный трехмерный поток жидкости, не обладающей вязкостью, может сформировать хаотические линии тока.

В 1984 г. X. Ареф из Университета Брауна обнаружил, что уравнения, описывающие траектории частиц жидкости в двумерном потоке, формально идентичны уравнениям, описывающим гамильтоновы системы. Развивая это наблюдение путем компьютерного моделирования, он доказал, что в гамильтоновой системе под действием периодически меняющихся сил может происходить эффективное перемешивание.

Если в трехмерном случае прямой связи между перемешиванием и гамильтоновой системой не существует, для двумерных систем эта связь однозначна: перемешивание жидкости можно рассматривать как наглядное проявление хаотического поведения гамильтоновой системы. Работа Арефа и простота лабораторного изучения двумерных систем по сравнению с трехмерными вдохновили меня на эксперименты по наблюдению признаков хаоса. Мы использовали специальный прибор для изучения потоков в замкнутой полости, который был сконструирован в 1983 г. совместно с моими студентами в Амхерсте.

Фотографирование

Студенту-дипломнику К. Ленгу и мне удалось определить приблизительное расположение нескольких периодических точек и крупномасштабных структур в двумерном потоке с помощью фиксирования стробоскопических изображений исследуемой системы (поскольку нас интересовало быстрое перемешивание, основное внимание уделялось поведению периодических точек низкого порядка, т. е. с периодом один, два, три; точки более высокого порядка участвуют в процессе намного реже). В типичном эксперименте пробные капли флуоресцирующего красителя вводились в определенные места прямоугольной полости, которая освещалась ультрафиолетовым излучением; стенки полости приводились в заданное движение и затем положения капель и искажение их формы фотографировались через равные промежутки времени.

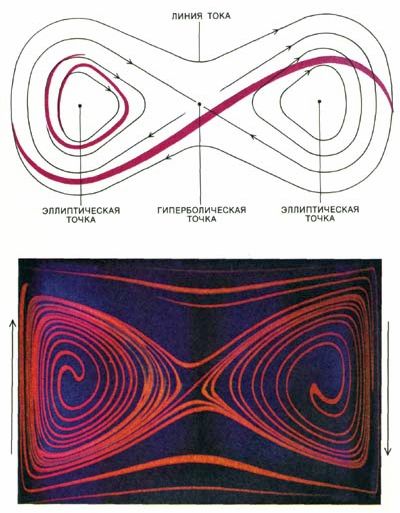
Рис 4. ЭЛЛИПТИЧЕСКИЕ И ГИПЕРБОЛИЧЕСКИЕ ТОЧКИ типичны для медленных двумерных потоков. Такой поток показан на снимке внизу, сделанном Ленгом и автором статьи. Поток глицерина в прямоугольной полости инициировался движением двух ее боковых стенок в противоположных направлениях с постоянной скоростью. Оранжевые полосы пробной жидкости (располагавшейся в начальный момент времени по диагонали от нижнего левого угла до верхнего правого угла полости) почти соответствуют линиям тока, т. е. линиям, по которым движутся частицы жидкости в стационарном потоке. На фотографии потока видны три фиксированные точки: центральная гиперболическая и две эллиптические по обе стороны от нее. Вокруг каждой эллиптической точки (вверху) образуются водовороты, вращающиеся по часовой стрелке. При движении вокруг этих точек длина оранжевой полосы растет пропорционально времени. К гиперболической точке жидкость течет в одном направлении, а от нее — в другом. Поскольку жидкость не может пересекать линии тока, подобные стационарные потоки неэффективны для перемешивания. Однако, если поток изменять во времени, оранжевый след пробной жидкости не будет успевать подстраиваться за меняющимися линиями тока, и на нем быстро образуются складки при изменении направления потока.

Если перемешивание шло эффективно, то окрашенные частицы распространялись по большому участку системы, если нет — краситель переходил из капли в остальную часть системы медленно или сами пробные капли оставались вблизи эллиптических периодических точек.

В другой серии экспериментов, которые мы выполнили со студентом-дипломником П. Свэнсоном, основное внимание было сконцентрировано на потоках, для которых существуют точные аналитические решения уравнений движения жидкости. Это давало наилучшую возможность сравнить экспериментальные результаты с предсказаниями теории.

К сожалению, число систем, для которых получены точные аналитические решения, довольно невелико, и многие из них настолько сильно идеализированы, что воспроизвести их в условиях лабораторного эксперимента невозможно. Одна из систем, допускающая точное решение и пригодная для эксперимента, представляет собой поток между двумя вращающимися эксцентрическими цилиндрами.

Такая система исследовалась также Арефом (сейчас он работает в Калифорнийском университете в Сан-Диего) и М. Тейбором и Р. Шевре из Колумбийского университета.

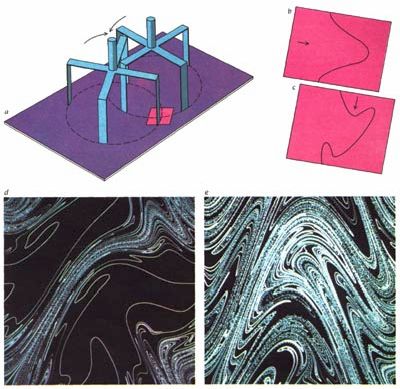
Рис 5. МОДЕЛЬ МИКСЕРА, разработанная Дж. Франьоном и автором статьи, иллюстрирует основной процесс перемешивания — вытягивание и образование складок (а). Линия, нарисованная на плоской ячейке жидкости, вытягивается и изгибается, образуя складки, когда нож миксера пересекает ее сначала в направлении перпендикулярном ей (b), а затем — параллельном ей (с). Линия вытягивается не разрываясь. Любой ее участок, покидающий ячейку, возвращается с противоположной стороны. Перемешивание в такой системе может быть смоделировано на компьютере. Внизу показаны компьютерные изображения линии, состоящей из 100 000 точек после 16 циклов перемешивания в разных условиях. Перемешивание может быть ограничено отдельными участками ячейки (d) или может охватить всю ячейку (е) в зависимости от того, насколько «энергично» оно проводилось.

Многочисленные эксперименты с двумерными хаотическими потоками показали, что крупномасштабные структуры в перемешиваемой жидкости (такие как положения и формы «островов» и крупных складок) хорошо воспроизводимы; более мелкие детали этой вытянуто-складчатой структуры невоспроизводимы. Причина заключается в том, что небольшой разброс начальных положений окрашенных капель быстро растет на хаотических участках потока. Так и должно быть: точное воспроизведение рассматриваемого процесса перемешивания невозможно. В конце концов перемешивание приводит к полной хаотичности. Именно это и достигается с помощью процедуры вытягивания и образования складок, которая применялась в наших экспериментах.

Интересно также, как в таком потоке могут сосуществовать хаос и симметрия, связанная с периодическими точками. Систематически исключая симметрию из хаотического потока, нам удалось повысить эффективность перемешивания.

Сравнение результатов экспериментов и компьютерного моделирования

Достаточно простую экспериментальную систему (для которой можно вычислить поле скоростей) легко смоделировать на компьютере. Типичная программа заключается в том, что некоторое число пробных точек помещают в моделируемое поле скоростей. Вычисленные положения точек после около 1000 периодов дают хорошую общую картину поведения системы по истечении длительного времени. Изображение, полученное в результате такого моделирования, называют сечением Пуанкаре. Если сечение Пуанкаре выглядит достаточно сложно, его считают доказательством наступления хаоса (см. верхний рисунок справа). Компьютерное моделирование процесса перемешивания обнаруживает также черты необратимости, но в этом случае невоспроизводимость обусловлена экспоненциальным ростом ошибки, вносимой компьютером, поскольку он может обрабатывать числа только с конечным количеством знаков.

Если возможно компьютерное моделирование перемешивания, то зачем утруждать себя физическими экспериментами? Не следует забывать

Рис 6. ВЯЗКИЙ ПОТОК в подшипнике скольжения, т. е. поток в зазоре между двумя вращающимися эксцентрическими цилиндрами тоже может быть смоделирован на компьютере. При периодическом вращении цилиндров в противоположных направлениях поток жидкости приводит к хаотическому перемешиванию. Это видно на сечении Пуанкаре для системы после 1000 периодов (вверху) и по картине растяжений после 10 периодов (внизу). Сечение Пуанкаре получено путем введения нескольких окрашенных «частиц» в моделируемый поток перемешиваемой жидкости. После каждого периода частицы переводились в новое, вычисленное на компьютере положение. На картине растяжений видны белые области — это участки жидкости, вытянутые моделируемым потоком. Цветные области — участки, где растяжение незначительно. Приведенная картина растяжений очень похожа на структуру, создаваемую реальным потоком (см. рисунок на обложке журнала). Снимки сделаны П. Свэнсоном и автором статьи в Амхерсте.

основное: при компьютерном моделировании этого процесса разрешение по скорости должно быть намного выше, чем при моделировании многих других задач гидродинамики. Даже весьма простые поля скоростей способны создать чрезвычайно сложные структуры (см. рисунки 1 и 2); в некоторых задачах о перемешивании желательно, чтобы выявлялись самые тонкие детали образующейся структуры.

Например, при моделировании потока в прямоугольной полости поле скоростей, вычисленное обычным образом, может оказаться слишком неточным для выявления деталей вытянуто-складчатой структуры. Оно оказывается практически бесполезным для точного нахождения координат периодических точек, определяющих сложное поведение хаотических потоков. Кроме того, если для большинства задач гидродинамики вычисление поля скоростей служит конечной целью, в задаче о перемешивании — это только начальная стадия.

По этой причине исследование процесса перемешивания проводилось в основном на весьма схематичных потоках (описываемых уравнениями, которые в некоторых случаях могут быть решены точно), а не на более близких к реальности системах, для которых может быть получено лишь приблизительное решение. Действительно, численные методы, с помощью которых получают приблизительные решения гидродинамических уравнений, часто служат источником ложных эффектов, отсутствующих в реальной задаче о перемешивании жидкостей.

Даже компьютерное моделирование простых потоков, которые мы проводили, часто приводило к непреодолимым трудностям. Компьютер представляет жидкость как совокупность дискретных элементов. При этом окрашенная капля может состоять из сотен тысяч элементов, и число операций, выполняемых компьютером в процессе слежения за ее хаотическим поведением при перемешивании, может быть огромным.

Чтобы проследить за поведением всех полос в областях хаотического перемешивания даже в случае простого примера (показанного на рис.1-2), потребовалось бы 300 лет машинного времени на компьютере с быстродействием миллион операций в секунду в режиме с плавающей точкой. Несомненно, можно оспаривать необходимость детального слежения за отдельными элементами структуры, считая более оправданным рассматривать структуру статистически. Но не будет ли это означать признания поражения? Если поле скоростей (или «движение») точно известно, то зачем обращаться к статистическим методам?

Таким образом, новые теоретические исследования нуждаются в объединении с хорошо поставленными экспериментами, поскольку, вероятнее всего, прямые вычисления не могут дать ответ на многие вопросы, касающиеся хаотических потоков. Например, каким образом должны двигаться стенки полости с жидкостью для того, чтобы размеры «островов» (включая и вновь образующиеся) стали меньше некоторой заданной величины? Ответ на этот вопрос позволил бы в будущем создать весьма тонкую систему, которая могла бы анализировать структуру смешивающейся жидкости, обнаруживать «острова» и менять поток так, чтобы они смешивались с остальной жидкостью.

Рекомендуем скачать другие рефераты по теме: новые сочинения, мировая экономика.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата