Предыдущая страница реферата | 1  2

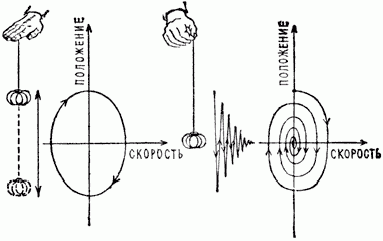
Рис. 2.

Фазовое пространство – это, с одной стороны, абстрактное математическое пространство, координатами в котором служат положения и скорости всех точек физической системы, а с другой стороны, оно очень удобно для наглядного описания ее эволюции. Например, движение шарика на абсолютно упругой резинке, в которой нет трения, полностью определяется начальной скоростью и положением шарика (начальными условиями). Каждому мгновенному состоянию такого осциллятора – колебательной системы – отвечает точка на фазовой плоскости. Когда шарик колеблется вверх и вниз без трения, эта точка описывает замкнутую кривую, а если колебания постепенно затухают, то фазовая траектория сходится по спирали к предельной точке, соответствующей остановке шарика. Эта точка неподвижна: если шарик подтолкнуть, его фазовая кривая вернется в ту же точку, которая как бы притягивает все близлежащие траектории. Поэтому ее называют неподвижной притягивающей точкой, или фокусом. Такая притягивающая точка – простейший тип аттрактора.

Что же дает изображение процессов в фазовом пространстве? А вот что: только взглянув на «фазовый портрет» физической системы, мы можем заявить, находится она в состоянии равновесного или неравновесного порядка. Более того, несмотря на их разную физическую сущность, эти два вида порядка можно изобразить на одной и той же диаграмме в виде четких точек, линий и фигур. Можно также нарисовать диаграмму перехода из одного упорядоченного состояния в другое.

А всегда ли геометрические образы на фазовой диаграмме будут четкими? Оказывается, что существует класс явлений, противоположных порядку как по физической сущности, так и по характеру изображения на фазовой диаграмме. Их образы размыты, нечетки, носят случайный, или, как говорят, стохастический характер. Явления, порождающие такие образы, называются хаотическими.

Что такое «хаос»?

Когда в июле 1977 года Нью-Йорк внезапно погрузился во тьму, никто даже не предполагал, что причина катастрофы – переход энергетической системы города из равновесного состояния в хаотическое, вызванный дисбалансом выработки и потребления энергии. Неожиданно из энергетической системы города выпал крупный потребитель. Система автоматики и диспетчерская служба не успели отключить эквивалентную этому потребителю, по существу, работающую только на него, генерирующую станцию. Образовался разрыв между генерацией энергии и ее потреблением, и в результате энергетическая система перешла из состояния равновесия в хаотическое. «Фазовый портрет» системы с одной частотой (в США эта частота равна 60Гц), которая поддерживается с высокой точностью, превратился в портрет с огромным числом частот – «размылся». Ситуация непрерывно ухудшалась, так как система защиты потребителей от случайных, хаотических «бросков» напряжения и сбоя частоты начала последовательно отключать предприятия от источников энергии. Это была самая настоящая катастрофа – развал системы. Такие катастрофы довольно редки, однако практически ежедневно в крупных энергосистемах мира наблюдаются явления не столь опасные, но все же доставляющие немало хлопот. В линиях передачи «гуляют» случайные, хаотические частоты, вызванные переменами в режиме работы оборудования и несовершенством систем управления. Они наносят экономике ущерб не меньший, чем потери на сопротивление в линиях передачи – «джоулево тепло», на которое расходуется около 20 процентов вырабатываемой в мире электроэнергии.

Обычно под хаосом всегда понималось неупорядоченное, случайное, непрогнозируемое поведение элементов системы. Многие годы господствовала теория, утверждавшая, что статистические закономерности определяются только числом степеней свободы: полагали, что хаос – это отражение сложного поведения большого количества частиц, которые, сталкиваясь, создают картину неупорядоченного поведения. Наиболее характерный пример такой картины – броуновское движение мелких частиц в воде. Оно отражает хаотические тепловые перемещения громадного числа молекул воды, случайным образом ударяющих по плавающим в воде частицам, вынуждая их к случайным блужданиям. Такой процесс оказывается полностью непредсказуемым, недетерминированным, поскольку точно установить последовательность изменений в направлении движения частицы невозможно – мы ведь не знаем, как движутся все без исключения молекулы воды. Но что отсюда следует? А вот что: становится невозможным вынести такие закономерности, которые позволяли бы точно прогнозировать каждое последующее изменение траектории частицы по предыдущему ее состоянию. Иными словами, не удается надежно, достоверно связать между собой причину и следствие или, как выражаются специалисты по математической физике, формализовать причинно-следственные связи. Такой вид хаоса можно назвать недетерминированным (НХ). И все же некоторые усредненные характеристики поведения в состоянии недетерминированного хаоса были найдены. Используя аппарат статистической физики, ученые сумели вывести формулы, описывающие кое-какие обобщенные параметры броуновского движения, например, расстояние, пройденное частицей за некоторое время (первым эту задачу решил А.Эйнштейн).

Однако в самые последние годы внимание исследователей все больше сосредоточилось на так называемом детерминированном хаосе (ДХ). Этот вид хаоса порождается не случайным поведением большого количества элементов системы, а внутренней сущностью нелинейных процессов. (Именно такой хаос и привел к энергетической катастрофе в Нью-Йорке.) Оказывается, что детерминированный хаос – отнюдь не редкость: всего два упруго сталкивающихся бильярдных шара образуют систему, сложная поведенческая функция которой имеет статистические закономерности, то есть содержит элементы «хаоса». Отталкиваясь друг от друга и от стенок бильярдного стола, шары рассеиваются под разными углами, и через некоторую последовательность соударений их можно рассматривать как неустойчивую динамическую систему с непрогнозируемым поведением. Аналитические решения нелинейных уравнений, описывающих поведение таких систем, как правило, не могут быть получены. Поэтому исследования проводятся с помощью вычислительного эксперимента: на ЭВМ шаг за шагом получают численные значения координат отдельных точек траектории.

В фазовом пространстве детерминированный хаос отображается непрерывной траекторией, развивающейся во времени без самопересечения (иначе процесс замкнулся бы в цикл) и постепенно заполняющей некоторую область фазового пространства. Таким образом, любую сколь угодно малую зону фазового пространства пересекает бесконечно большое количество отрезков траектории. Это и создает в каждой зоне случайную ситуацию – хаос: И вот что удивительно: несмотря на детерминизм процесса – ведь бильярдные шары полностью подчиняются классической, «школьной» механике, – ход его траектории непредсказуем. Другими словами, мы не в состоянии предвидеть или хотя бы грубо охарактеризовать поведение системы на достаточно большом отрезке времени и в первую очередь потому, что принципиально отсутствуют аналитические решения.

Порядок на сковородке

Если налить на сковороду тонкий слой какой-нибудь вязкой жидкости (например, растительного масла) и нагревать сковороду на огне, поддерживая температуру масляной поверхности постоянной, то при слабом нагреве – малых тепловых потоках – жидкость остается спокойной и неподвижной. Это типичная картина состояния, близкого к равновесному порядку. Если сделать огонь побольше, увеличивая тепловой поток, то через некоторое время – совершенно неожиданно – вся поверхность масла преображается: она разбивается на правильные шестигранные или цилиндрические ячейки. Структура на сковороде становится очень похожей на пчелиные соты. Это замечательное превращение называется явлением Бенара, по имени французского исследователя, одним из первых изучившего конвективную неустойчивость жидкости.

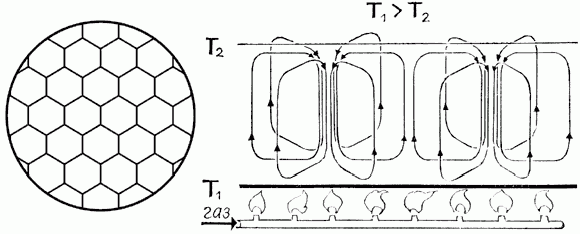
Рис. 3.

Конвективные ячейки Бенара. В 1900 году была опубликована статья французского исследователя Бенара с фотографией структуры, по виду напоминавшей пчелиные соты. При нагревании снизу слоя ртути, налитой в плоский широкий сосуд, весь слой неожиданно распадался на одинаковые вертикальные шестигранные призмы, которые впоследствии были названы ячейками Бенара. В центральной части каждой ячейки жидкость поднимается, а вблизи вертикальных граней опускается. Иными словами, в сосуде возникают направленные потоки, которые поднимают нагретую жидкость (с температурой T1) вверх, а холодную (с температурой T2) опускают вниз.

Если и дальше увеличивать тепловой поток, то ячейки разрушаются – происходит переход от порядка к хаосу (П→Х). Но самое удивительное заключается в том, что при еще больших тепловых потоках наблюдается чередование переходов:

Х→П→Х→П→...!

При анализе этого процесса в качестве параметра, который показывает, когда на сковороде будет «порядок» и когда «хаос», то есть определяющего «зону» порядка или хаоса, выбирается так называемый критерий Рэлея, пропорциональный разности температур вверх по слою масла. Этот параметр называют управляющим, поскольку он «управляет» переводом системы из одного состояния в другое. При критических значениях Рэлея (математики называют их точками бифуркации) и наблюдаются переходы «порядок – хаос».

Нелинейные уравнения, которыми описывается образование и разрушение структур Бенара, называются уравнениями Лоренца. Они связывают между собой координаты фазового пространства: скорости потоков в слое, температуру и управляющий параметр.

Процессы, происходящие в сосуде, могут быть зафиксированы, например, киносъемкой и сопоставлены с результатами вычислительного эксперимента. На рис.4 показано именно такое сопоставление. Совпадение результатов физического и вычислительного экспериментов поразительно! Но прежде, чем перейти к анализу этих результатов, нам придется еще раз обратиться к фазовому пространству.

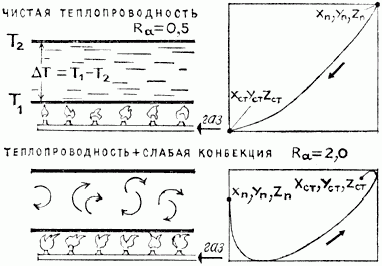
Рис. 4а.

Переходы от порядка к хаосу на примере явления Бенара. Управляющим параметром, который играет роль «ручки регулировки», здесь служит так называемый критерий Рэлея (Re), пропорциональный разности температур вверх по слою жидкости. «Вращение» этой регулирующей ручки соответствует большему или меньшему нагреву жидкости. При слабом нагреве (Re

Скачали данный реферат: Chernyh, Belov, Лисов, Головнин, Караваев, Rytin.
Последние просмотренные рефераты на тему: реферат по философии, реферати українською, контрольные 8 класс, конспект по окружающему миру.

Предыдущая страница реферата | 1  2