Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

 .

Т.о. математический аппарат современной квантовой механики ориентирован на вычисления вероятностей пребывания физических систем в тех или иных состояниях и средних значений физических величин, характеризующих эту систему, т.е. как раз те величины, которые могут быть измерены в реальном эксперименте.

Эволюция во времени квантово-механических систем. Для описания изменения системы во времени вводится оператор эволюции, связывающий ее состояния в два близких момента:

 .

Если оператор эволюции известен, его последовательное применение к исходному состоянии системы позволяет проследить за ее временным развитием, т.е. решить основную задачу естествознания. Обычно оператор эволюции за бесконечно малый промежуток времени записывают в виде

,

где - оператор Гамильтона. Подстановка выражения (9) в (8) приводит к основному уравнению квантовой механики

 ,

играющему столь же важную роль в квантовой теории, как законы Ньютона в классическом естествознании. По своему смыслу оператор Гамильтона является обобщением классического понятия энергии, поскольку для частного случая стационарной изолированной системы  (где энергия сохраняется) уравнение (10) имеет решение

,

совпадающее с волной ДеБройля и удовлетворяющее стационарному уравнению

.

Стационарные состояния квантово-механических систем.

При решении уравнения (11) определяются стационарные состояния системы и соответствующие им значения энергии W. В случае дискретного набора разрешенных энергий говорят об энергетических уровнях системы, в случае непрерывного набора - о непрерывном спектре энергий. Например, базисные состояния  и  молекулы бензола не являются стационарными: являющаяся следствием соотношения неопределенности неточная локализация электронов в пространстве приводит к возможности перехода этих состояний друг в друга (т.н. туннельный эффект). Уравнение (12) позволяет отыскать два сохраняющихся во времени состояния, которые оказываются симметричной и антисимметричной линейными комбинациями базисных:

 ,

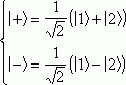и определить соответствующие им энергии

 .

Т.о. наличие возможности переходов между двумя эквивалентными состояниями приводит к возникновению в системе двух энергетических уровней вместо одного (рис. 20_3). Система может находиться лишь в одном из построенных стационарных состояний (  ), но в каждом из них вероятность найти классически осмысленную конфигурацию  или  одинакова и равна 0.5. Симметричное стационарное состояние энергетически более выгодно и наиболее часто реализуется в природе.

Аммиачный мазер. Существует множество разнообразных систем, обладающих двумя базисными состояниями, не сохраняющимися во времени. К ним относится молекула аммиака, с классической точки зрения имеющая две конфигурации  или , способные превращаться друг в друга из-за туннельного эффекта (рис. 20_4). Стационарные энергетические уровня молекулы разделены зазором, энергетически соответствующем высокочастотному радиоизлучению. Настроенное в резонанс внешнее электромагнитное поле способно вызывать переходы между этими состояниями, которых сопровождаются поглощением или излучением энергии в виде электромагнитных волн (на другом языке - фотонов). Ансамбль из молекул, находящихся в верхнем энергетическом состоянии способен только излучать энергию, т.е. взаимодействовать с электромагнитным полем, усиливая его. На описанном принципе основана работа первого мазера - лазера, работающего в радио диапазоне излучения.

Природа химической связи. Системой с двумя состояниями является простейшее химическое соединение - молекулярный ион водорода  (рис. 20_5). Как и в рассмотренных выше случаях причиной не сохранения во времени выбранных базисных состояний является туннельный эффект. При сближении ядер вероятность туннельного перехода электрона от одного к другому возрастает , что приводит к увеличению расстояния между подуровнями и делает симметричное состояние иона энергетически более выгодным. “Стремясь к снижению полной энергии”, ядра сближаются, что воспринимается как результат действия дополнительной силы, обеспечивающей возникновение химической связи.

Природа электростатических и ядерных взаимодействий. В общих чертах сходный механизм лежит в основе современных представлений о возникновении электростатических взаимодействий между электрическими зарядами. Вместо “туннелирующего” электрона в молекулярном ионе роль переносчика электрических взаимодействий между зарядами играют виртуальные фотоны, обнаружения которых в реальном эксперименте оказывается принципиально невозможным.

Сходный механизм был предложен и в случае сильных ядерных взаимодействий. Быстрый спад ядерных сил при увеличении расстояний привел к допущению, что переносчиком взаимодействия является на обладающий нулевой массой покоя фотон, а весьма тяжелая частица с массой, превосходящей электронную примерно в 200 раз. Вскоре такие частицы были обнаружены в космических лучах (пи-мезоны), но дальнейшие эксперименты показали их непричастность к ядерным силам. Однако выдвинутая гипотеза все же оказалась жизнеспособной: впоследствии были обнаружены похожие на ранее открытые мезоны частицы, свойства которых согласовывались с предсказанными на основе анализа ядерных сил.

Электропроводность кристаллов. Системы с двумя состояниями обладают двумя энергетическими подуровнями . Увеличение числа эквивалентных состояний приводит к появлению большего числа подуровней. Примером системы с большим числом состояний может служить электрон в идеальном кристалле, который может быть локализован вблизи каждого из N регулярно расположенных ионов, что соответствует набору базисных состояний:  (рис. 20_6). Самой низкой энергии соответствует симметричная линейная комбинация базисных состояний:

 ,

другие ортогональные линейные комбинации дают систему из близкорасположенных друг к другу N энергетических подуровней. При увеличении числа атомов в кристалле подуровни сливаются в сплошную полосу - энергетическую зону, соответствующую непрерывному набору разрешенных значений энергии электрона. Поскольку свободная частица в пустом пространстве так же может обладать энергией из непрерывного набора, поведение электрона в идеальном бесконечном кристалле весьма сходно с поведением свободной частицы. Этим объясняется возможность существования электропроводности в твердых кристаллических телах.

Уравнение Шредингера. При описании движения микрочастиц в пространстве в качестве базисного удобно выбрать непрерывный набор состояний с определенными координатами , для каждого из которых может быть записано уравнение, аналогичное (10). Конкретный вид оператора Гамильтона для этого случая был правильно угадан Шредингером и имеет вид, аналогичный классическому выражению для механической энергии:

Рекомендуем скачать другие рефераты по теме: реферат бесплатно на тему, реферат на тему творчество.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата