Структурная надежность систем

| Категория реферата: Рефераты по науке и технике
| Теги реферата: реферат по географии, конспект подготовительная группа
| Добавил(а) на сайт: Kazarinov.

Предыдущая страница реферата | 18 19 20 21 22 23 24 25 26 27 28 | Следующая страница реферата

18. Расчет показывает (таблица 7.1), что при

ч для элементов преобразованной схемы (рис. 7.4)

. Следовательно, из трех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент F (система “2 из 4” в исходной схеме (рис. 7.1)) и именно увеличение его надежности даст максимальное увеличение надежности системы в целом .

19. Для того, чтобы при ч система в целом имела вероятность безотказной работы , необходимо, чтобы элемент F имел вероятность безотказной работы (см. формулу (7.9))

(7.11)

При этом значении элемент F останется самым ненадежным в схеме (рис. 7.4) и рассуждения в п.18 останутся верными.

Очевидно, значение , полученное по формуле (7.11), является мини-мальным для выполнения условия увеличения наработки не менее, чем в 1.5 раза, при более высоких значениях увеличение надежности системы будет большим.

20. Для определения минимально необходимой вероятности безотказной работы элементов 12 - 15 (рис. 7.1) необходимо решить уравнение (7.6) относительно при . Однако, т.к. аналитическое выражение этого уравнения связано с определенными трудностями , более целесообразно использовать графо-аналитический метод. Для этого по данным табл. 7.1 строим график зависимости . График представлен на рис. 7.6.

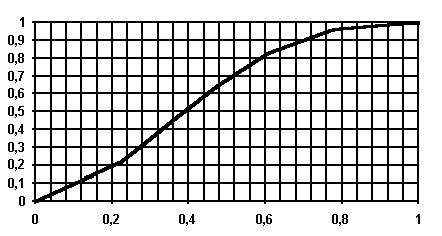
Рис. 7.6. Зависимость вероятности безотказной работы системы “2 из 4” от вероятности безотказной работы ее элементов.

21. По графику при находим .

22. Так как по условиям задания все элементы работают в периоде нормальной эксплуатации и подчиняются экспоненциальному закону (7.10), то для элементов 12 - 15 при находим

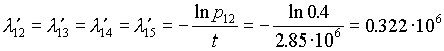ч. (7.12)

23. Таким образом, для увеличения - процентной наработки ситемы необходимо увеличить надежность элементов 12, 13, 14 и 15 и снизить интенсивность их отказов с до ч, т.е. в 1.55 раза.

24. Результаты расчетов для системы с увеличенной надежностью элементов 12, 13, 14 и 15 приведены в таблице 7.1. Там же приведены расчетные значения вероятности безотказной работы системы “2 из 4” F` и системы в целом P`. При ч вероятность безотказной работы системы , что соответствует условиям задания. График приведен на рис 7.5.

25. Для второго способа увеличения вероятности безотказной работы системы - структурного резервирования - по тем же соображениям (см. п. 18) также выбираем элемент F, вероятность безотказной работы которого после резервирования должна быть не ниже (см. формулу ( 7.11 )).

26. Для элемента F - системы “2 из 4” - резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов невозможно, т.к. число элементов должно быть целым и функция дискретна.

27. Для повышения надежности системы “2 из 4” добавляем к ней элементы, идентичные по надежности исходным элементам 12 - 15, до тех пор, пока вероятность безотказной работы квазиэлемента F не достигнет заданного значения.

Для расчета воспользуемся комбинаторным методом (см. раздел 3.3) :

- добавляем элемент 16, получаем систему “2 из 5”:

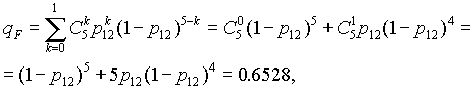(7.13)

(7.14)

- добавляем элемент 17, получаем систему “2 из 6”:

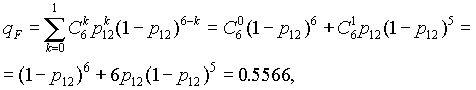(7.15)

(7.16)

- добавляем элемент 18, получаем систему “2 из 7”:

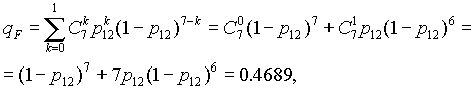(7.17)

(7.18)

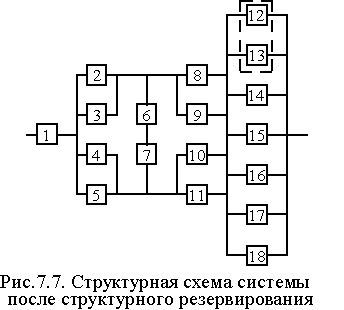
28. Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме (рис. 7.1) систему “2 из 4” достроить элементами 16, 17 и 18 до системы “2 из 7” (рис. 7.7).

29. Результаты расчетов вероятностей безотказной работы системы “2 из 7” F`` и системы в целом P`` представлены в таблице 7.1.

30. Расчеты показывают, что при ч , что соот-ветствует условию задания.

31. На рис. 7.5 нанесены кривые зависимостей вероятности безотказной работы системы после повышения надежности элементов 12 - 15 (кривая ) и после структурного резервирования (кривая ).

Выводы:

1. На рис. 7.5 представлена зависимость вероятности безотказной работы системы (кривая ). Из графика видно, что 50% - наработка исходной системы составляет часов.

2. Для повышения надежности и увеличения 50% - наработки системы в 1.5 раза (до часов) предложены два способа:

а) повышение надежности элементов 12, 13, 14 и 15 и уменьшение их отказов с до ч;

б) нагруженное резервирование основных элементов 12, 13, 14 и 15 идентичными по надежности резервными элементами 16, 17 и 18 (рис. 7.7).

3. Анализ зависимостей вероятности безотказной работы системы от времени (наработки) (рис. 7.5) показывает, что второй способ повышения надежности системы (структурное резервирование) предпочтительнее первого, так как в период наработки до часов вероятность безотказной работы системы при структурном резервировании (кривая ) выше, чем при увеличе-нии надежности элементов (кривая ).

Таблица 6.1

Численные значения параметров к заданию

№

Интенсивности отказов элементов, l i , x10-6 1/ч

вар.

0.1

1.0

0.5

1.0

0.1

0.2

0.5

1.0

0.1

1.0

2.0

1.0

5.0

0.2

0.05

1.0

0.5

0.2

0.02

0.01

0.05

Рекомендуем скачать другие рефераты по теме: ответы гиа, конспект.

Claw.ru | Рефераты по науке и технике | Структурная надежность систем

Структурная надежность систем

Категории:

Поделитесь этой записью или добавьте в закладки

Рефераты от А до Я

Полезные заметки