Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Также рассматриваются два процесса активной спектроскопии: прямые четырехфотонные процессы и каскадные трехфотонные процессы, связанные с нелинейными восприимчивостями c (3) и c (2) соответственно. Первые работы в данной области были начаты еще в конце 60-х годов [2]. Эта часть исследования представляет наибольший интерес, так как спектроскопия неравновесных состояний способна дать значительно больше информации в отличие от других методов, которые имеют гораздо меньшую величину полезного сигнала на выходе из исследуемого объекта. Исследованы особенности четырехволновых процессов рассеяния света на поляритонах для создания оптимальной спектроскопической схемы, позволяющей проводить измерения дисперсии поляритонов. Далее результаты четырехволновой методики сравниваются с дисперсией поляритонных состояний, полученной по спектрам трехволнового рассеяния света на поляритонах.

Глава 1. Рассеяние света на равновесных поляритонах.

§ 1 Рассеяние света в однородных кристаллах.

Параметрическое рассеяние света представляет собой процесс спонтанного распада фотонов накачки (w L, kL) в кристалле с отличной от нуля квадратичной восприимчивостью на сигнальный (w S, kS) и холостой фотоны (w P, kP), либо фотон и поляритон. Волновые векторы и частоты при стоксовом рассеянии удовлетворяют следующим условиям :

, (1)

которые являются законами сохранения импульса и энергии. Частоты собственных механических колебаний кристаллической решётки имеют тот же порядок колебаний, что и частоты инфракрасных электромагнитных волн: от 1011 до 1013 Гц (10-3000 см-1 ). При определенных условиях возможно прямое взаимодействие оптических колебаний решетки с инфракрасными электромагнитными волнами, т.е. существование поляритонных волн.

1.1 Дисперсионная кривая кристалла.

Основные черты частотно-углового спектра СПР определяются дисперсионной кривой w (k) кристалла. Дисперсионное соотношение кубического (неанизотропного) кристалла в гармоническом приближении в однорезонансном случае имеет вид:

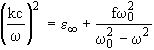, (2)

где e - диэлектрическая проницаемость среды на частотах много больших фундаментальных частот кристаллической решётки, но много меньших частот электронных переходов, f=e 0-e - сила осциллятора, w 0 - фундаментальная частота оптического колебания решетки. На рис.1 приведена дисперсионная кривая соответствующая уравнению (2). Если бы поперечные механические колебания и электромагнитные волны были независимы, то первые описывались

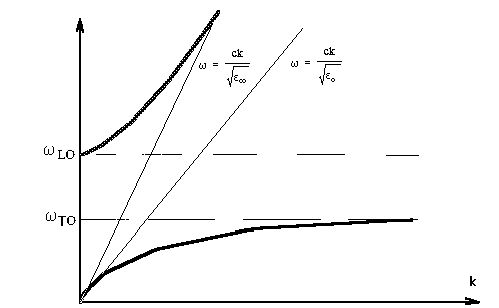
Рис.1 Дисперсия кубического кристалла.

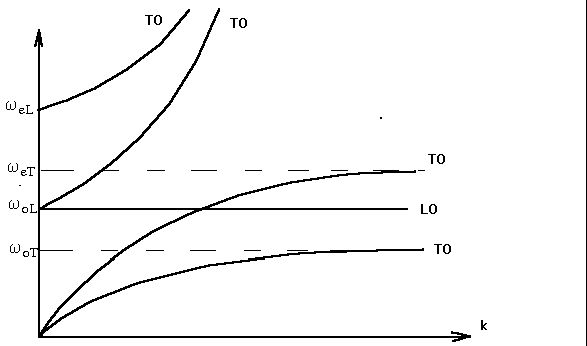
Рис.2 Дисперсия анизотропного кристалла.

бы прямыми .w (k)=w TO и w (k)=w LO, а вторые - прямой w =. Запаздывающее взаимодействие между этими колебаниями в кристалле приводит к поляритонным возбуждениям, имеющим смешанную электромеханическую природу. На частотах, больших w LO находиться верхняя поляритонная ветвь. На частотах между w TO и w LO находится запрещенная зона, где среда не прозрачна для объемных волн.

В анизотропных одноосных кристаллах частотам поперечных и продольных колебаний w Т и w L соответствуют частоты колебаний, смещения которых параллельны (w еТ; w еL) и перпендикулярны (w оТ; w оL) оптической оси. На рис.2 изображены дисперсионные кривые, соответствующие случаю, когда вектор перпендикулярен главной оптической оси кристалла.

1.2. Интенсивность СПР и симметрия кристалла LiNbO3.

Впервые вопрос об интенсивности СПР рассматривался в работе [3]. Когда поляритонная частота w p далека от частоты фонона, достаточно рассматривать квадратичную нелинейную восприимчивость c (2). Будем рассматривать накачку, как плоскую монохроматическую волну с интенсивностью SL и предположим, что углы рассеяния q p,s на частотах w p, w s малы, так что , где А - сечение рассеивающего объёма V, l - длина кристалла. Тогда мощность, рассеиваемая на частоте w s в направлении в единичный спектральный и угловой интервалы, равна[4]:

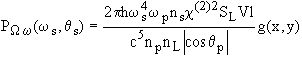(3)

где - свертка тензора c (2) и ортов поляризации соответствующих волн, ns,p,L - показатели преломления на соответствующих частотах, а 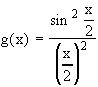- форм-фактор, описывающий частотно-угловую структуру СПР, когда среда прозрачна на всех трёх частотах. В последнем выражении введено обозначение ,.где - отстройка волнового вектора поляритона от точного синхронизма.

Рекомендуем скачать другие рефераты по теме: диплом, уголовное право шпаргалки.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата