Удивительные свойства упаковочной пленки

А.Л. Волынский, член-корреспондент РАН, д.х.н., проф., гл.н.с.

Иногда случается так, что хорошо известные и изученные предметы и явления вдруг открываются новыми и необычными сторонами. Именно это произошло при исследовании упаковочной полимерной пленки на нашей кафедре. Казалось бы, что в ней особенного? Это просто упаковочный материал, без которого быт современного человека совершенно немыслим: металлизированные полимерные пленки (как правило, с тонким алюминиевым слоем) используют, например, для упаковки цветов, продуктов, промышленных товаров, применяют в полиграфии и во многих других областях. Неудивительно, что такие полимерные материалы выпускаются сегодня сотнями тысяч тонн.

Вполне естествен и интерес самых разных специалистов к столь распространенным в быту и промышленности объектам. Уже многие годы издается журнал “Thin Solid FILMs” (“Тонкие твердые пленки”), где освещаются научные и прикладные аспекты проблем, связанных с изучением и использованием систем, которые можно обозначить как “твердое покрытие на податливом основании”.

Удивительно, что при всем том научном интересе, который проявляют исследователи к подобным системам, до недавнего времени никому не пришло в голову просто растянуть упаковочную армированную пленку (она как раз и представляет собой типичную систему “твердое покрытие на податливом основании”) и посмотреть, что из этого получится. А посмотреть, как оказалось, есть на что: в микроскоп (сканирующий электронный) видны ряды светлых полос с регулярным волнистым рельефом, разделенных темными полосами.

Что это за ряды и каким образом они появляются?

Растягивая полимерную пленку, на которую твердое покрытие нанесено тонким слоем, мы растягиваем одновременно и этот слой. В результате покрытие распадается на множество “островов”-фрагментов. Они-то и “выстраиваются” рядами, образуя своеобразный рельеф. Поражает регулярность самопроизвольно возникающего рельефа и его строгая ориентация относительно оси растяжения: его углубления и вершины всегда ориентированы строго параллельно оси. Высока и степень порядка, достигаемая при фрагментации покрытия: образующиеся острова однородны по размерам и располагаются на поверхности податливой подложки весьма регулярным образом. Другими словами, на растянутой полимерной пленке возникают высокоорганизованные периодические структуры. Именно поэтому деформированная упаковочная пленка рассеивает свет, как настоящая дифракционная решетка.

А всегда ли проявляются подобные результаты растяжения? Может быть, они зависят от природы подложки (полимера) и покрытия? Мы это выяснили, взяв для экспериментов один и тот же полимер, но с разным покрытием, и наоборот - одно покрытие на разных полимерах.

Микрофотографии трех видов растянутых пленок, армированных разными металлами.

Ось растяжения показана стрелкой. Увел. (слева направо): в 350 раз, 1100 и 1750.

Никакой зависимости мы не обнаружили, всякий раз возникали уже знакомые нам структуры. Правда, необходимо было соблюдать два условия:

- толщина покрытия должна быть пренебрежимо малой по сравнению с толщиной подложки;

- модуль упругости покрытия должен на несколько порядков превышать этот показатель для материала подложки. Именно таким требованиям соответствует упаковочная пленка [1, 2].

Теперь вполне правомочен вопрос: каким образом при простом растяжении возникает столь регулярная структура? Попробуем разобраться в механизме наблюдаемого явления. Примем во внимание, что полимерная пленка, подвергаемая одноосному растяжению, испытывает одновременно два вида деформации - удлинение и сжатие в перпендикулярных друг другу направлениях. (В этом легко может убедиться каждый, растягивая кусок резиновой ленты.) Следовательно, твердое покрытие на поверхности пленки тоже растягивается и сжимается одновременно. Именно сжатием покрытия, как выясняется, обусловлено возникновение регулярного микрорельефа. Какова же физическая суть этого процесса?

Покрытие, представляющее собой анизодиаметричное твердое тело (т.е. с очень разными размерами в перпендикулярных направлениях), испытывает деформацию одноосного сжатия на поверхности растягиваемой полимерной пленки. Надо сказать, что впервые явления, сопровождающие одноосное сжатие анизодиаметричных твердых тел, были рассмотрены Л.Эйлером более 200 лет назад. Он показал, что тело при достижении критической нагрузки теряет устойчивость и приобретает форму полуволны (так называемая эйлеровская классическая потеря устойчивости). Подобное легко наблюдать, сжимая, например, тонкую металлическую линейку или лист бумаги. Если же анизодиаметричное твердое тело (в нашем случае это тонкое жесткое покрытие) прочно связать с податливой подложкой (основанием), то картина потери им устойчивости решающим образом изменяется. При достижении критической сжимающей нагрузки тело не сможет принять форму полуволны, так как при отклонении от прямолинейной формы на него будет действовать со стороны подложки возвращающая сила, пропорциональная величине отклонения. В результате такого взаимодействия противоборствующих сил покрытие неизбежно сложится, подобно складному метру, и примет синусоидальную форму с периодом волны, равным l.

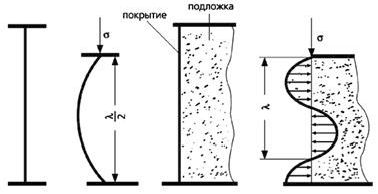
Схема потери устойчивости анизодиаметричного тела в свободном состоянии (а, б) и на податливом основании (в, г).

Величина периода волны (рельефа) определяется следующим. Работа деформации при сжатии анизодиаметричного твердого тела - покрытия - растет с увеличением числа совершенных изгибов (с уменьшением периода рельефа). Не случайно, что без подложки такое тело принимает форму полуволны, т.е. период рельефа максимален. Однако податливая, но весьма протяженная подложка вносит поправки в этот процесс. Очевидно, что чем больше период рельефа, тем, при прочих равных условиях, больше его амплитуда. Полимерная подложка не остается безучастной к ее увеличению - она “течет”, деформируется. Энергетические затраты всей системы при этом стремятся к минимизации. Период рельефа можно найти из условия минимума общего баланса напряжений в покрытии и подложке.

Такого рода минимизация энергии системы в случае упругой каучуковой подложки дает величину периода рельефа

l = 4.15h·(E1/E)1/3, (1)

где h - толщина покрытия, E1 и Е - модули упругости покрытия и подложки соответственно.

Если же подложка пластична, период рельефа равен

l = 2hsy /s, (2)

где sy - предел текучести покрытия, s - предел текучести подложки при растяжении. Расчеты для того и другого случая экспериментально подтверждены. Хорошее соответствие теории и эксперимента свидетельствует о разумности предположений, сделанных относительно механизма возникновения регулярного рельефа на поверхности упаковочной пленки.

Регулярность фрагментации жесткой оболочки связана, кроме того, с особенностями передачи механического напряжения от податливого основания твердому покрытию через границу раздела. Здесь необходимо отметить, что характер самой фрагментации зависит, в частности, от того, однородно или неоднородно деформируется подложка. Полимерные пленки могут деформироваться обоими путями. Хотя деформация подложки достигается разными способами, регулярность фрагментации твердого покрытия оказывается неизбежной.

Рекомендуем скачать другие рефераты по теме: рефераты на украинском языке, компьютерные рефераты.





1  2  3 | Следующая страница реферата