Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



Рисунок 7.1 - структурная схема усилителя с направленным ответвителем

Принципиальная схема усилителя с (НО) приведена в приложении В.

8. МЕТОДИКА РАСЧЕТА МКЦ.

Важным вопросом, при построении как широкополосных так и полосовых усилителей мощности, является вопрос получения максимального усиления от каждого усилительного каскада при заданном допустимом уклонении АЧХ от требуемой формы. Это связано с тем, что уменьшение усиления приводит: к снижению коэффициента полезного действия усилителя, из-за возрастания числа усилительных каскадов и увеличения потребляемой ими мощности от источника питания; к ухудшению линейности амплитудной характеристики и возрастанию интермодуляционных искажений, вследствие работы предоконечных каскадов усилителей на частотно-зависимое сопротивление нагрузки при повышенных выходных напряжениях.

В [7] описана методика параметрического синтеза таблиц нормированных значений элементов КЦ используемых в усилителях мощности, позволяющая осуществлять их реализацию с максимально возможным коэффициентом усиления при заданном допустимом уклонении АЧХ от требуемой формы.

Используя однонаправленную модель транзистора, передаточную функцию каскада с КЦ можно описать дробно-рациональной функцией комплексного переменного:

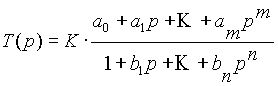(1)

где - нормированная частота; - текущая круговая частота; - высшая круговая частота полосы пропускания широкополосного усилителя, либо центральная частота полосового усилителя; К - множитель определяющий уровень коэффициента передачи; - коэффициенты, являющиеся функциями параметров КЦ нормированных относительно и сопротивления источника сигнала для широкополосных и для полосовых усилителей.

Выберем в качестве прототипа передаточной характеристики каскада дробно-рациональную функцию вида:

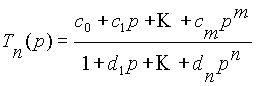. (2)

Найдём такие её коэффициенты, которые позволят из системы нелинейных уравнений:

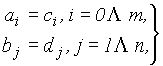
(3)

рассчитать нормированные значения элементов КЦ, обеспечивающие максимальный коэффициент усиления при заданном допустимом уклонении АЧХ от требуемой формы. С целью нахождения требуемых значений коэффициентов перейдем к квадрату модуля функции (2):

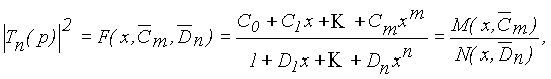
где -вектор коэффициентов ; -вектор коэффициентов

Для решения задачи нахождения векторов коэффициентов воспользуемся методом оптимального синтеза теории фильтров. Для этого составим систему линейных неравенств:

(4)

,

где - дискретное множество конечного числа точек в заданной нормированной области частот; - требуемая зависимость квадрата модуля на множестве ;- допустимое уклонение от ; малая константа .

Первое неравенство в (4) определяет величину допустимого уклонения АЧХ каскада от требуемой формы. Второе и третье неравенства определяют условия физической реализуемости рассчитываемой КЦ. Учитывая, что полиномы и положительны, модульные неравенства можно заменить простыми и записать задачу в следующем виде :

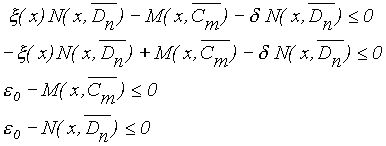(5)

В результате получим систему однородных линейных неравенств, являющуюся задачей линейного программирования. Для обеспечения максимального коэффициента усиления рассчитываемого каскада, неравенства (5) следует решать при условии максимизации функции цели:Решение неравенств (5) дает векторы коэффициентов , соответствующие заданным и. Коэффициенты ,соотношения (2), определяются по известным корням уравнений [5]:

Далее, из решения системы нелинейных уравнений (3), находятся нормированные значения элементов КЦ, обеспечивающие максимальный коэффициент усиления каскада при заданном допустимом уклонении АЧХ от требуемой формы.

Многократное решение системы линейных неравенств (5), для различныхи, позволяет осуществить синтез таблиц нормированных значений элементов КЦ, по которым ведется проектирование усилителей.

В качестве примера осуществим синтез таблиц нормированных значений элементов одной из наиболее простых и эффективных КЦ применяемых в полосовых усилителях мощности, схема которой приведена на рис.1.

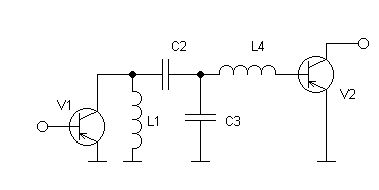
Рис. 8.1.

Аппроксимируя входной и выходной импедансы транзисторов V1 и V2 RC- и RL-цепями, от схемы приведённой на рис. 1 перейдём к схеме приведённой на рис.2.

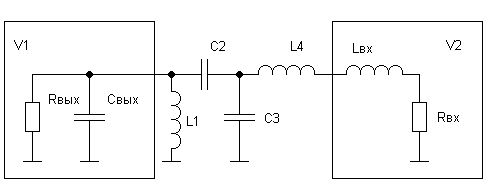
Рис. 8.2.

Вводя идеальный трансформатор после конденсатора С2, с последующим применением преобразования Нортона, перейдём к схеме представленной на рис.3.

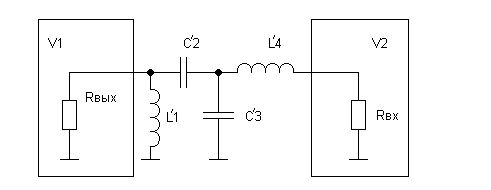
Рис. 8.3.

Коэффициент прямой передачи последовательного соединения КЦ и транзистора V2, c учётом преобразования КЦ (рисунок 3), можно описать выражением:

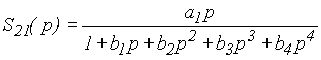, (6)

где ; - коэффициент усиления транзистора V2 по мощности в режиме двустороннего согласования на частоте ;

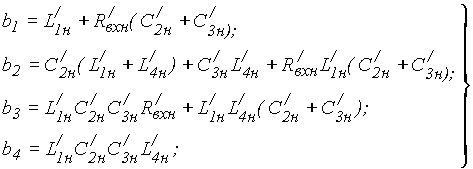(7)

(8)

- нормированные относительно и значения элементов .

По известным значениям , переходя от схемы на рис 3 к схеме на рис.2, найдём:

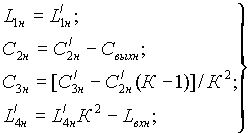(9)

где , - нормированное относительно и значение .

Из (6) следует, что коэффициент усиления каскада в полосе пропускания равен:

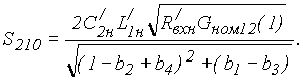(10)

Соотношения (7) - (9) позволяют рассчитать нормированные значения элементов схемы (рис.1) по известным коэффициентам b1, b2, b3, b4. Для нахождения указанных коэффициентов сформируем квадрат модуля функуции-прототипа передаточной характеристики рассматриваемой цепи:

Рекомендуем скачать другие рефераты по теме: реферат сфера, электронный реферат.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата