Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Важное обстоятельство, которое позволяет выделить феномен волн-убийц в отдельную научную и практическую тему и, соответственно, отделить от других явлений, связанных с волнами аномально большой амплитуды (например, цунами), — появление волн-убийц из «ниоткуда». В отличие от цунами, возникающих в результате подводных землетрясений и оползней, появление волн-убийц не связано с катастрофическими геофизическими событиями. Эти волны могут появляться при малых ветрах и относительно слабом волнении, что приводит к идее о том, что само явление волн-убийц связано с особенностями динамики самих морских волн и их трансформации при распространении в океане. Следовательно, вопрос о вероятности появления этих волн может быть сформулирован как вопрос о физических механизмах, повышающих эту вероятность. Закономерно возникает и следующий вопрос — на какие физические процессы образования волн-убийц следует прежде всего обратить внимание?

Простейший физический механизм формирования волн-убийц может быть исследован довольно просто в рамках линейной теории поверхностных волн. Линейность задачи, в частности, означает, что результатом совпадения двух независимых возмущений будет сумма этих возмущений (принцип линейной суперпозиции). Поверхностные волны (волны на воде) являются диспергирующими волнами, т.е. скорости их распространения зависят от их периода (длины волны). В глубоком океане (длина волны много меньше его глубины) фазовая скорость С волны длиной l дается выражением:

С = (gλ/(2))1/2 .

Поэтому гребни волн с различными периодами (длинами), распространяясь с разными скоростями, могут совпасть в определенный момент в некоторой точке пространства и дать, в принципе, сколь угодно большой всплеск (рис. 4). Вероятность такого события ничтожно мала и очень сильно зависит от некоторого начального распределения амплитуд (энергий) отдельных волновых компонент. Именно с помощью задания граничных условий определенного вида такая волна-убийца может быть легко получена в лабораторных условиях — частота волнопродуктора уменьшается по специальному закону таким образом, чтобы быстрые низкочастотные волны догнали высокочастотные относительно медленные волны в нужной точке — точке фокусировки [12]. Максимальная высота волны в точке фокусировки в рамках линейной теории ничем не ограничена, ограничения связаны с нелинейными процессами, в частности с обрушением достаточно крутых волн.

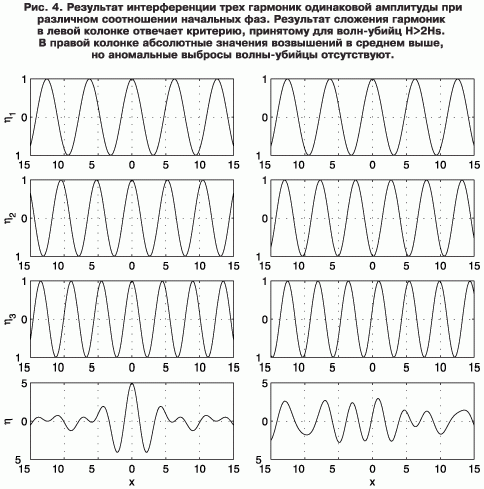
Волны-убийцы, возникающие в результате такой фокусировки, очевидно, будут короткоживущими — быстро сбежавшиеся волновые гребни (впадины) так же быстро разбегутся. Эта особенность наблюдается для реальных волн-убийц и подтверждается результатами численного моделирования в рамках слабонелинейной теории и численного решения полных уравнений гидродинамики.

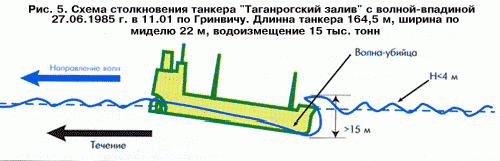
Интересно, что волны, возникающие в результате линейной фокусировки, могут быть как волнами возвышения, так и волнами-впадинами. Волны-убийцы, имеющие вид впадин, довольно часто наблюдаются в океане и представляют серьезную опасность для судов из-за трудности их своевременного обнаружения. Одна из встреч с такой волной описана в работе [13]. При вполне обычной погоде и волнении 3-4 балла танкер «Таганрогский залив» неожиданно «провалился» (рис. 5). Палуба, возвышавшаяся над уровнем спокойного моря на высоте 7 м, была залита слоем воды более двух метров. Один из матросов, работавших в это время на баке, был тяжело травмирован. Инцидент произошел у побережья Южной Африки вблизи стрежня течения Агульяс.

Области морских течений рассматриваются как области наиболее вероятного появления волн-убийц [14]. Неоднородности течения (равно как и неоднородности рельефа дна) могут служить своеобразными линзами, фокусирующими волновую энергию в определенных областях. Характерная картина фокусировки-дефокусировки волн прибрежными течениями и неоднородностями глубины показана на рис. 6. Такая фокусировка не повышает частоты возникновения волн-убийц, как это определяется формальным критерием (1), но она, очевидно, способна существенно увеличить абсолютные амплитуды волн, а значит, и возможные катастрофические последствия столкновения с этими волнами.

Для того чтобы наглядно представить себе, как работают два описанных выше линейных механизма образования волн-убийц, рассмотрим простую аналогию. В любом месте большого города возможно аномально большое скопление народа. Локальное увеличение плотности людей относительно некоторой средней плотности является аналогом возникновения волны-убийцы с помощью первого из описанных нами механизмов. Однако абсолютная величина плотности таких локальных скоплений будет неодинаковой в разных местах города. Очевидно, волны-убийцы наибольшей абсолютной амплитуды будут возникать в тех местах, где люди «фокусируются» тем или иным образом (торговые центры, вокзалы и т.п.).

Нелинейность морских волн, по-видимому, принципиальным образом влияет на вероятность появления волн-убийц. В результате нелинейности эффект сложения первоначально независимых возмущений может существенно отличаться от их простой суммы — компоненты ветрового волнения могут интенсивно обмениваться между собой энергией. Принципиальный физический эффект, связанный с нелинейностью волн, — возможность формирования волновых пакетов и уединенных волн, т.н. солитонов. Отдельные нелинейные волны (группы) могут распространяться на значительные расстояния без существенного изменения формы. Именно с нелинейностью морских волн связано то, что волны-убийцы могут образовываться не только в виде внезапного всплеска, но и существовать в течение относительно большого времени, увеличивая тем самым вероятность столкновения с судами и морскими сооружениями.

В приближении слабой нелинейности механизмы трансформации поверхностных волн изучены достаточно хорошо. Качественно нелинейность приводит к тому, что между элементарными гармониками появляется взаимодействие, гармоники обмениваются энергией, в результате чего эффект при их совпадении может быть сильнее или слабее. На языке рассмотренной выше аналогии с толпой увеличение плотности покупателей в отдельных местах (в очереди за особо привлекательным товаром) может приводить к «отталкиванию» (некоторые люди не любят больших очередей) или к «притяжению», когда становится возможным катастрофическое нарастание плотности (давка, драки и т.п.).

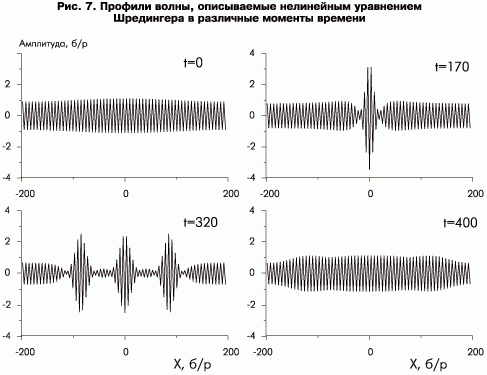
Наиболее известным слабонелинейным эффектом является модуляционная неустойчивость поверхностных волн (неустойчивость Бенджамена-Фейра). Две близкие по частоте волны могут сближаться из-за того, что их скорости различны (эффект частотной дисперсии), однако эти скорости зависят еще и от амплитуд волн — чем выше амплитуда, тем выше скорость распространения нелинейной волны (амплитудная дисперсия). Игра частотной и амплитудной дисперсии приводит к тому, что процесс будет повторяться квазипериодически — длинная волна, догоняя короткую, теряет энергию, а значит, скорость, и начинает отставать. Такой процесс описывается нелинейным уравнением Шредингера (2), которое является универсальным и применяется во многих областях современной физики:

. (2)

Один из сценариев поведения решений такого уравнения показан на рис. 7. Характер решений принципиальным образом определяется безразмерным параметром — крутизной волны:

ε = 2А/λ ,

где A — характерная амплитуда волны. Характерный масштаб модуляций (периодические осцилляции амплитуд волн) имеет порядок ε, т.е. каждые 1/ε периодов интенсивность волнения будет достигать некоторого максимума. Это явление периодического изменения амплитуды волн хорошо известно морякам и всем, кто видел картину И. Айвазовского «Девятый вал». Крутизна морских волн (исключая волны-убийцы) даже в самых суровых штормовых условиях редко превышает 0,1, и 9-е (10-е, 11-е и т.д.) валы очень хорошо чувствуются людьми, страдающими морской болезнью.

Эффекты сильной нелинейности морских волн изучены недостаточно хорошо. Физические модели, допускающие детальный математический анализ, в этом случае практически отсутствуют, и основными инструментами исследования являются эксперименты (лабораторный и морской) и численное моделирование.

Сценарий образования волн-убийц в этом случае может быть представлен следующим образом [15,16]. При относительно малой крутизне волн и первоначально однородном волновом поле происходит развитие модуляционной неустойчивости, которая может приводить к появлению устойчивых квазистационарных волновых пакетов. Сталкиваясь, такие пакеты могут образовывать пакеты большей амплитуды и, далее, уединенные волны — солитоны. По достижении некоторой критической амплитуды такие солитоны могут становиться неустойчивыми и обрушиваться. Сценарий, подобный описанному, неоднократно наблюдался. Волны-убийцы в некоторых случаях распространяются группами из небольшого числа очень крутых волн. В качестве иллюстрации упомянем случай, описанный капитаном Фредерик-Моро — командиром учебного крейсера ВМС Франции «Жанна д'Арк» [17].

5 февраля 1963 г. крейсер «Жанна д'Арк» находился в 430 милях к юго-востоку от Токио. Был западный ветер 15-20 м/с, волнение 7 баллов с запада высотой 7-8 м. Корабль находился в дрейфе, курс 2 румба относительно направления волнения; заданный курс 245-250°, причем рулевой с трудом удерживал судно на заданном курсе. Один из винтов был незадолго до этого поврежден; винт правого борта позволял поддерживать скорость хода 4 узла.

В 09.47 судового времени впереди по курсу была замечена группа больших обрушивающихся волн сразу за полосой относительно спокойной воды (высота волн 4-5 м). Капитан немедленно скомандовал «25 градусов влево» для того, чтобы встретить волны наиболее выгодным образом и уберечь единственный работающий винт. Судно успело повернуться на 15° и встретило первую волну по направлению 2 румба к борту; высота волны была около 15 м.

Эта волна бросила судно влево таким образом, что оно оказалось во впадине волны с дифферентом около 15° и сильным креном около 30° на правый борт. Судно повернулось еще на 20° влево. Капитан скомандовал «прямо руля» и затем «25 градусов вправо». В провале между первой и второй волнами судно почти встало на ровный киль, но было настигнуто второй волной, положившей судно на правый борт с креном около 35°. Во время выхода из крена левый (высокий) борт находился под водой. Вахтенные видели плавающими спасательные буи, закрепленные на второй палубе; один из буев был потерян. Третья волна имела несколько меньшую амплитуду и была пройдена относительно легко.

Инцидент с «Жанной д'Арк» известен как «Великолепная тройка». В описании этого случая эксперты отмечают следующие характерные черты:

Рекомендуем скачать другие рефераты по теме: реферат реформы, экзамен.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата