Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

После того, как рассчитан коэффициент детерминации по однофакторной модели, в нее включают следующий факторный признак, у которого коэффициент парной корреляции выше, чем у других оставшихся факторных признаков. Проверку того, насколько точнее описывает изменение результативного признака двухфакторная модель, проводят с помощью критерия Фишера: Fрасч= D1 / D2 , где D1 и D2 - остаточные дисперсии, рассчитанные по одно- и двухфакторным моделям, причем D1>D2. Расчетную величину критерия Фишера сравнивают с табулированным значением для степеней свободы f=n-k-1, где n - число наблюдений, k - число факторных признаков. Сама величина остаточной дисперсии вычисляется по формуле Dj= (е(y^ – y)2) /( n-k-1), где y^ и y - соответственно расчетное и текущее значение изучаемого показателя. Если Fрасч > Fтабл, то уравнение, обеспечивающее меньшую остаточную дисперсию, существенно точнее описывает динамику изучаемого показателя. В противном случае существенность отличия моделей друг от друга не подтверждается и лучше использовать более простую модель.

При любом варианте событий (включается ли второй факторный признак или нет) переходят к следующему факторному признаку, и процедура расчетов повторяется.

Коэффициент детерминации показывает долю вариации результативного признака, обусловленную всеми включенными в модель факторными признаками. Если в модели присутствует несколько факторных признаков, то влияние каждого из них рассчитывается по выражению (8):

d y(i) = (ai * (еyj *xj(i)) /n - ysr *x sr(i))/(sy)2,

где dy(i) - доля i-го факторного признака в вариации результативного признака y (частный коэффициент детерминации), ai - коэффициент в уравнении множественной регрессии при xi, n - количество объектов в рассматриваемой совокупности, yj , *xj(i) - текущие значения результативного и i-го факторного признаков, ysr, xsr(i) - средние арифметические значения соответственно результативного и i-го факторного признаков, (sy)2 - дисперсия результативного признака.

Возможно использование формулы

d y(i) = ai * (n*еyj * xj(i) -- еyi *е xj(i))/( еyj2 -еyj*еyj).

В том и другом случае суммирование ведется по j, где j - номер объекта в совокупности (j=1, 2,…, n).

Cумма частных коэффициентов детерминации равна коэффициенту детерминации D, который в свою очередь равен квадрату коэффициента (индекса) корреляции. Суммирование производится по i :

D = еd y(i) .

Второй метод определения факторных признаков, вводимых в модель, основан на исключении из общей модели, где присутствуют все факторные признаки, тех, которые подвержены мультиколлинеарности. Формализованные в большей или меньшей степени, эти способы исключения (например, упоминавшийся выше подход Фаррара и Глаубера) решающее слово оставляют за самим исследователем.

В нашей работе использован метод пошагового включения факторных признаков.

Эконометрические модели производственных функций, основанные на линейной зависимости

Для всех рассматриваемых групп полиграфических предприятий (предприятия в целом; газетные предприятия; книжно-журнальные предприятия) характерно, что наибольшую корреляцию с размерами выручки демонстрирует фактор численности работающих, а наименьшую - фактор производственной площади. Это свидетельствует о том, что до настоящего времени именно живой, а не овеществленный труд играет главенствующую роль в российских типографиях.

Однофакторные линейные модели обычно интерпретируют таким образом, что коэффициент при аргументе показывает, на сколько единиц увеличится значение результативного признака, если значение факторного признака возрастет на единицу.

Если следовать этому правилу, то увеличение штата персонала на одного работника принесет газетным предприятиям в среднем 178,71 тыс. руб. дополнительной выручки, книжно-журнальным - 219,32 тыс. руб., а по всем предприятиям в целом 203,10 тыс.руб. При этом коэффициент детерминации оказывается самым большим по группе книжно-журнальных предприятий (0,924), меньше других - по группе газетных предприятий (0,579). Для группы всех предприятий он составил 0,874.

Введение второго факторного признака - собственного капитала - увеличивает детерминацию моделей: по группе книжно-журнальных предприятий на 2,8 процентных пункта, по газетным предприятиям - на 9,7 процентных пункта, по группе всех предприятий - на 3,0 процентных пункта. При этом происходит перераспределение обусловленности вариации результативного признака между факторными признаками, включенными в модель.

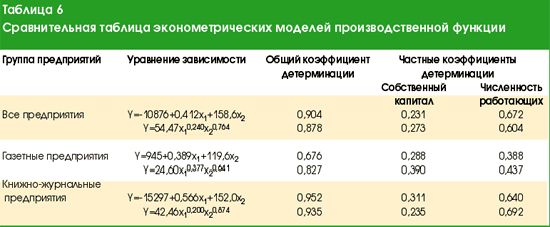
Так, в однофакторной модели по группе всех предприятий 87,4% всех изменений выручки объяснялось изменением численности работающих. В двухфакторной же модели "ответственность" за вариацию результативного фактора передается частично фактору собственного капитала. За счет этого частная детерминация фактора численности работающих снижается до 67,2%. Коэффициент парной корреляции между факторными признаками довольно велик - 0,780 (табл.3), и это означает, что определенная мультиколлинеарность имеет место. Однако характерно то обстоятельство, что при введении в экономическую модель двух факторов, каждый из них "теряет в весе" по сравнению с однофакторной моделью неодинаково: фактор численности, как уже отмечалось,с 87,4 до 67,2%, то есть на 20,2 процентных пункта, а фактор собственного капитала - с 70,1 до 23, 1%, или на 47,0 процентных пунктов. То же самое наблюдается и по группам газетных и книжно-журнальных предприятий. Следовательно, можно говорить, что двухфакторные модели дают более объективную картину, нежели однофакторные в части определения уровня влияния факторных признаков, но небольшое увеличение коэффициента общей детерминации свидетельствует о том, что с ростом числа факторных признаков качество модели улучшается незначительно.

Об этом же говорит и то, что лишь для группы книжно-журнальных предприятий введение в модель третьего фактора привело к увеличению коэффициента общей детерминации, и то только на 0,4 процентных пункта, что в принципе находится в зоне погрешности эксперимента, и серьезных выводов на этом измерении строить нельзя.

Таким образом, при использовании линейной формы производственной функции и трех рассмотренных факторных признаков рационально рассматривать двухфакторную эконометрическую модель зависимости выручки от факторов численности работающих и собственного капитала.

Эконометрические модели производственных функций, основанные на степенной зависимости

В отличие от моделей, построенных на линейных зависимостях, модели, использующие степенную функцию, существуют исключительно в области положительных значений результативного признака, если масштабирующий коэффициент а0, входящий в уравнение, больше 0. Если а0 < 0, модель просто неприменима.

Как и в случае линейных зависимостей, наибольшую коррелированность с результативным признаком показывает фактор численности работающих, а наименьшую - фактор производственных площадей. Введение второго факторного признака (собственный капитал) сильнее всего увеличивает уровень детерминации по группе газетных предприятий, в существенно меньшей степени по группам книжно-журнальных и всех предприятий. С добавлением третьего фактора (производственные площади) степень детерминированности моделей снижается.

Исходя из этого в производственную функцию, формируемую на основе степенной зависимости, включаются два фактора: численность работающих и собственный капитал.

Рекомендуем скачать другие рефераты по теме: век реферат, военные рефераты.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата