Claw.ru | Промышленность, производство | Повышение рентабельности производства мяса крупного рогатого скота Повышение рентабельности производства мяса крупного рогатого скота | Категория реферата: Промышленность, производство | Теги реферата: риск реферат, план дипломной работы | Добавил(а) на сайт: Benedikt. Предыдущая страница реферата | 32  33  34  35  36  37  38  39  40  41  42 | Следующая страница реферата	1862,34
20. Яльчиковский	1914,42
10. Красночитайский	1919,9
6. Канашский	1938,86
17. Шемуршинский	1962,26
11. Марпосадский	1970,4
14. Урмарский	1978,47
8. Комсомольский	1980,09
3. Батыревский	1992,91
19. Ядринский	2016,03
15. Цивильский	2020,98
12. Моргаушский	2048,55

Изобразим ранжированный ряд распределения районов по ценам реализации 1 ц прироста живой массы крупного рогатого скота графически.

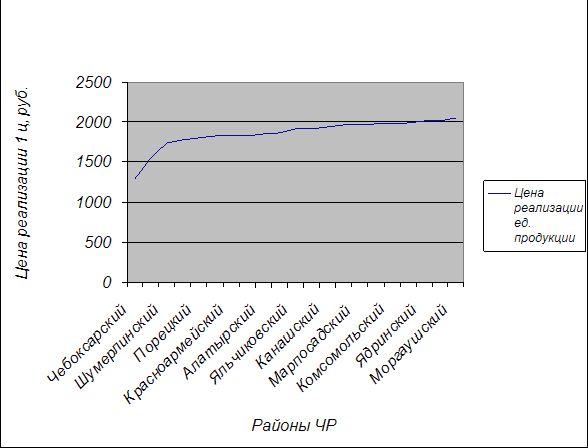
Рис.5. Ранжированный ряд распределения районов ЧР за 2002г. по ценам реализации 1 ц прироста живой массы КРС.

Построим интервальный ряд распределения районов: п=5, то h=(2048,55-1294,85)/5=150,74. Округлим до 151руб.

Таблица 19.

Интервальный ряд распределения районов ЧР за 2002 г. по ценам реализации 1 ц прироста мяса КРС.

Номер группы	Группа районов, руб.	Число районов
I	1294,85-1445,85	1
II	1445,85-1596,85	1
III	1596,85-1747,85	1
IV	1747,85-1898,85	7
V	1898,85-2049,85	11
	Итого	21

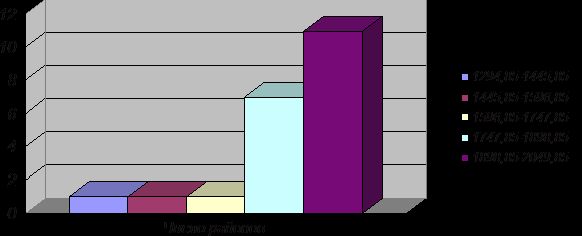
Рис.6. Графически изображенный интервальный ряд распределения районов по ценам реализации 1 ц прироста живой массы КРС.

Преобладающая доля районов реализует продукцию по высоким ценам. В пятую группу входят 12 районов ЧР с ценой реализации 1898,85-2049,85 руб. за 1 ц прироста живой массы крупного рогатого скота. По самой низкой цене за 1 ц мяса КРС в живой массе реализует Чебоксарский район и составляет 1294,85 руб. Во вторую и третью группу входят всего по одному району; это Козловский и Шумерлинский соответственно. Можно выделить следующие типические группы районов по ценам реализации:

I. (1294,85-1898,85)- 10района;

II. (1898,85-2049,85) – 11 районов.

На основе этих данных построим комбинационную таблицу. Проанализируем таблицу 20. В первой группе районов по себестоимости 1 ц привеса живой массы КРС до 2880 руб. реализуют по ценам меньше 1898,85 руб. 4 района (Чебоксарский, Вурнарский, Ибрессинский, Алатырский) и 6 районов – свыше 1898,85 руб/ц (Урмарский, Красночитайский, Цивильский, Комсомольский, Ядринский). В этой группу средний уровень окупаемости затрат равен 0,70 руб. Во 2 группе с себестоимостью от 2881 до 3429 руб/ц входят 6 районов, из них 3 района реализуют по цене до 1898,85 руб. и 3 района – свыше 1898,85 руб. Средний уровень окупаемости затрат во 2 группе составляет 0,79 руб. В третьей группе с себестоимостью свше 3430 руб/ц мяса КРС реализуют 5 районов, из них по цене до 1898,85 руб/ц 3 района (Красноармейский, Янтиковский и Козловский) и 2 района (Моргаушский и Канашский) – свыше цены 1898,85 руб/ц. Средний уровень окупаемости затрат в 3 группе составляет 0,87 руб.

3.3. Парная корреляция.

Каждое явление есть следствие многих факторов и причин, и в свою очередь каждое явление влияет на многие другие факторы. Изучит взаимосвязь между явлениями, значит:

1) установить направление взаимосвязи, т.е. направление воздействия одного явления на другое и если можно выразить это направление в виде уравнения;

2) измерит тесноту связи между явлениями.

Основной формой статистической связи является корреляционная связь. Корреляцией называется такая связь между двумя варьирующими признаками в статистической совокупности, при которой различием в величине одного из них соответствует закономерное различие между средними значениями другого. Корреляционный анализ применим к измерению связей между двумя признаками – парная корреляция или к измерению связей между тремя и большим числом признаков – множественная корреляция.

Простейшим и важнейшим из уравнений корреляционной связи является линейное уравнение. Парная корреляция всегда отражает лишь часть сложной системы взаимосвязей признака «х0». Парная корреляция результативного признака х0 с одним фактором х1 изучается как часть множественной корреляции.

Линейная парная связь между признаками выражается уравнением прямой:

Х0 = а0 + а1 х1,

где х0 – результативный признак,

х1 – факторный признак,

а0, а1 – параметры уравнения связи.

А0 – среднее значение х0 и не имеет экономического смысла. А1 – коэффициент регрессии, показатель силы связи факторного признака х0. Показывает среднее изменение результативного признака х0 при изменении факторного признака х1 на 1 его измерения. Параметры уравнения а0 и а1 находят методом наименьших квадратов. Для нахождения их составляют систему нормальных уравнений:

Теснота связи при различных формах зависимости определяется специальными показателями. При парной линейной зависимости – коэффициентом корреляции (r0;1), при множественной линейной корреляции – коэффициентом множественной корреляции (R0;1;2…n), при парной криволинейной зависимости – индексом корреляции.

Линейный парный коэффициент корреляции меняется в пределах от -1 до +1, а множественный коэффициент рассматривается только как положительная величина и изменяется в пределах от 0 до 1. Квадрат коэффициента корреляции называется коэффициентом детерминации и показывает, на сколько процентов результативный признак зависит от одного или нескольких факторных признаков, включенных в анализ.

15,937 = 21а0 + 67,01 а1 (1)

48,58 = 67,01а0 + 224,13а1 (2)

Вычтем (1) уравнение из (2) и получим:

32,643 = 46,01а0 + 157,12 а1

0,709 = а0 + 4,813а1

а0 = 0,709 – 4,813 а1

15,937 = 14,889 – 101,07а1 + 67,01а1

1,048 = -34,06а1

а1 = - 0, 03

а0 = 0,709 – 4,81 (-0,03) = 0,709 =0,144 = 0,853

17,913 – 2,0103 = 15,937

Уравнение парной линейной зависимости между уровнем окупаемости затрат на производство прироста мяса КРС и себестоимостью производства 1 ц привеса примет следующий вид: х0 = 0,853 – 0,03х1. Коэффициент регрессии (параметр а1) равный а1 = - 0,03, показывает, что с увеличением себестоимости производства 1 ц привеса живой массы КРС на единицу, уровень окупаемости затрат уменьшается на 0,03% в данных конкретных условиях. Для определения формы связи между уровнем окупаемостью затрат производства и себестоимостью 1 ц привеса живой массы КРС, построим график. На оси абсцисс нанесем значение независимой переменой (себестоимость 1 ц мяса КРС), на оси ординат – зависимой (уровня окупаемости затрат).

 

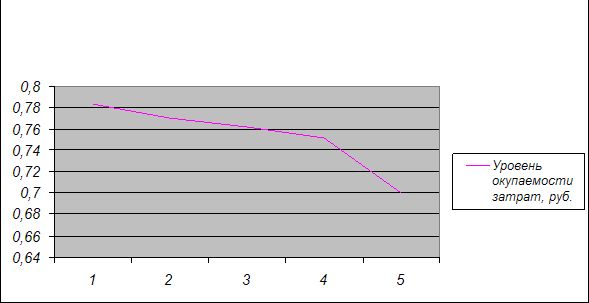
Рис 7. Связь уровня окупаемости затрат на производство привеса живой массы КРС и себестоимостью 1 ц привеса.

Определим тесноту связи между изучаемыми признаками, рассчитав коэффициент корреляции:

.

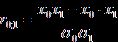Для определения коэффициента корреляции надо определить средние значения х0х1, х0 и х1, а также средние квадратические отклонения по результативному и факторным признакам.

х0х1 = (∑х0х1)/п=48,58/21 = 2,313

х0 = ∑х0 / п = 15,94 /21 = 0,758

х1 = ∑х1/_ + п = 67,01 / 21 = 3,2

рассчитаем средние квадратические отклонения:

σ0 = (∑(х0)2/ п – (х0)2) = 0,60 – 0,57 = 0,03 = 0,173

σ1 = (∑(х1)2/ п – (х1)2) = 10,67 -10,2 = 0,47 = 0,68 ,

полученные данные подставим в формулу и получим:

r0;1 = (2,313-2,42) / 0,121 = -0,107 0,121 = - 0,88, тогда коэффициент детерминации будет равен: r2=(-0,89)2= 0,77 или 77%, это значит, что уровень окупаемости затрат на 77% зависит от себестоимости, и на 23% - от других факторов, которые не были приняты во внимание.

3.4. Множественная корреляция.

Изменение экономических явлений происходит под влиянием не одного, а большего числа самых разнообразных факторов. Связь между результативным признаком и двумя и более факторами принято выражать уравнением множественной регрессии. Наиболее простым видом уравнения множественной регрессии – линейное уравнение с двумя независимыми переменными:

Х0 = а0 + а1х1 + а2х2. (3)

Параметры уравнения множественной регрессии определяется методом наименьших квадратов путем решения системы нормальных уравнений:

∑х0 = па0 + а1∑х1 +а2∑х2

∑х0х1 = а0∑х1 + а1∑(х1)2 + а2∑х1х2 (4)

Рекомендуем скачать другие рефераты по теме: тесты, шпора на пятке лечение.





Предыдущая страница реферата | 32  33  34  35  36  37  38  39  40  41  42 | Следующая страница реферата