Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата

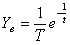
Изображение и оригинал реакции на единичную ступенчатую функцию запишутся в виде:

.

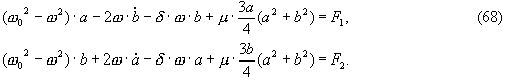Своеобразие экономических объектов, моделируемых инерционными звеньями, состоит в том, что в них накапливается разность вещественных единиц, из которых состоят входной и выходной потоки. Обозначим накопленное количество единиц через 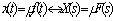. Тогда

,

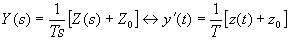где z0=z(0) – количество накопленных единиц в нулевой момент времени. Таким образом, при любом экзогенном воздействии и начальном состоянии звена z0 интенсивность (скорость, темп) выходного процесса инерционного звена пропорциональна текущему количеству накопленных единиц внутри звена. Коэффициент пропорциональности равен 1/T. Очевидно, что статистическое постоянство этого коэффициента в любых объектах экономики может служить признаком того, что динамической моделью объекта является инерционное звено.

5.Динамическая модель.

В этой главе будет рассмотрено взаимодействие интересующих нас субъектов в динамике с использованием математического аппарата преобразования Лапласа. Будут выведены ограничения на выделение помощи частным хозяйствам, при которых кооперативы не будут деградировать. Это пригодится нам в дальнейшем при синтезе математической модели, включающей в себя регламентирование отчислений в зависимости от распределения трудовых ресурсов.

5.1.Производственная функция и производственные фонды.

В процессе производства, с одной стороны, осуществляются капиталовложения и ввод производственных фондов в эксплуатацию. Этим процессом обусловлено увеличение количества производственных фондов. С другой стороны, происходит уменьшение производственных фондов в результате амортизации и выбытия. Если в качестве модели движения производственных фондов принять инерционное звено первого порядка, у котороко внешнее воздействие I(t) – интенсивность потока капиталовложений, S(t) – интенсивность потока амортизации и T – лаг эксплуатации производственных фондов, тогда текущая стоимость производственных фондов определяется операторным уравнением:

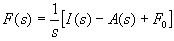,(1)

где F0 – начальная стоимость производственных фондов.

Запишем изображение процесса амортизации в виде:

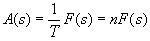,(2)

то есть амортизация пропорциональна текущей стоимости производственных фондов и составляет постоянную ее долю. Доля амортизированных фондов n – норма амортизации. Подставив реакцию A(s) в (1) и решив выведенное уравнение относительно F(s), получим следующую зависимость накопленного количества производственных фондов от капиталовложений:

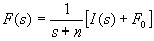.(3)

Предположим теперь, что производственная функция зависит только от стоимости производственных фондов, то есть является однофакторной. В данном случае следует абстрагироваться от трудовых ресурсов и прочих параметров, так как они не влияют на окончательный результат. Запишем однофакторную динамическую производственную функцию сельхозпредприятия:

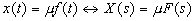,(4)

где m – фондоотдача.

Подставим в эту функцию полученное выражение для производственыых фондов и получим зависимость интенсивности выпуска от интенсивности потока капиталовложений в операторной форме:

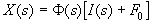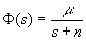, ,(5)

где F (s) – передаточная функция производственного звена.

5.2.Модель развития отдельного предприятия.

В синтезе модели отдельного предприятия будем исходить из того, что объем произведенной и реализованной продукции зависит от остаточной стоимости ОПФ, которая может увеличиваться или уменьшаться. Она возрастает в зависимости от капиталовложений и уменьшается в результате амортизации и выбытия некоторой части основных средств. Следовательно, рост объемов выпуска может быть обеспечен в том случае, если капиталовложения превышают количество изношенных ОПФ, тогда и текущая их стоимость увеличивается. При снижении стоимости ОПФ рост объема выпуска может быть достигнут за счет повышения фондоотдачи, то есть влияния научно-технического прогресса. Эти явления отражает модель производства в виде однофакторной динамической производственной функции.

Капиталовложения слагаются из централизованных средств I(t) и отчислений от дохода U(t). Предположим, что отчисления регламентируются нормативом a < 1. Тогда функциональную структуру развития предприятия можно представить в виде модели с положительной обратной связью, состоящей из двух звеньев. Усилительное звено 2 отражает процесс выделения собственных капиталовложений при нормативе отчислений от объема реализации продукции a. Вместе с централизованными капиталовложениями собственные средства воздействуют на звено производства 1, изменяя стоимость ОПФ и объем дохода от реализации продукции X(t) в видединамической производственной функции.

Чтобы найти передаточную функцию системы необходимо разрешить систему уравнений относительно X(s):

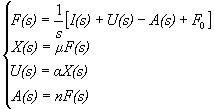(6)

Гдеn – норма амортизации,

Рекомендуем скачать другие рефераты по теме: текст для изложения, план курсовой работы.

Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата