Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Таким образом, распределение поля в плоскости вектора будет несколько отличаться от распределения в плоскости , что противоречит принятой зависимости распределения поля только от радиальной координаты. Однако вследствие небольшого различия между функциями  и  принятые допущения не приводят к существенным погрешностям в расчетах и в тоже время позволяют учесть различия в диаграмме направленности облучателя в плоскостях  и .

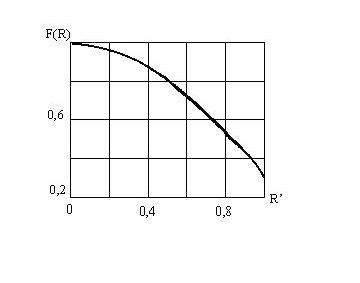Из рис. видно, что наиболее интенсивно облучается центр зеркала, а поле к его краям по амплитуде падает вследствие уменьшения значения  и увеличения  с увеличением . Типичное распределение нормированной амплитуды поля в раскрыве параболоидного зеркала показано на рис.:

Для упрощения последующих расчетов найденное значение целесообразно аппроксимировать интерполяционным полиномом

.

Этот полином хорошо аппроксимирует фактическое распределение поля в раскрыве параболоида и для нахождения поля излучения при такой аппроксимации не потребуется громоздких вычислений. Излучение круглой площадки с распределением поля на ее поверхности, определяемым, уже было рассмотрено выше.

Узлами интерполяции, т.е. точками, где полином  совпадает с ранее найденной функцией , будем считать точки раскрыва зеркала, соответствующие значениям :  Тогда коэффициенты полинома определяется из системы уравнений:

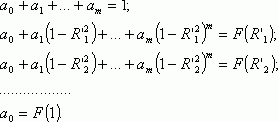
На этом решение задачи определения поля в раскрыве параболоида можно считать законченным.

При инженерных расчетах для упрощения вычислений обычно можно ограничиться тремя членами полинома, т.е. положить m=2. Тогда

В этом случае в качестве узлов интерполяции берут точки в центре раскрыва зеркала , на краю зеркала  и приблизительно в середине между этими крайними точками . Коэффициенты этого полинома определяются системой уравнений:

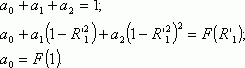
Относительная погрешность, определяющая отклонение полинома от заданной функции , может быть вычислена по формуле

.

Расчеты показывают, что во многих случаях уже при трех членах полинома относительная погрешность не превышает 1-2%. Если требуется большая точность, следует брать большее число членов полинома.

Б). Определение поля излучения параболоидного зеркала.

Раскрыв зеркала представляет собой плоскую круглую площадку. Поле на площадке имеет линейную поляризацию. Фаза поля в пределах площадки неизменна, а распределение амплитуды описывается полиномом .

Как было показано выше, каждый n-й компонент поля в раскрыве, представляемого полиномом, создает в дальней зоне напряженность электрического поля , где , S – площадь раскрыва, E0 – амплитуда напряженности электрического поля в центре площадки, ,  - ламбда-функция (n+1)-го порядка.

Полное поле в дальней зоне будет равно сумме полей, создаваемых каждым компонентом .

Выражение, определяемое суммой в последней формуле, представляет собой ненормированную диаграмму направленности антенны:

Для получения нормированной диаграммы направленности найдем максимальное значение . Максимум излучения синфазной площадки имеет место в направленности, перпендикулярном этой площадке, т.е. при . Этому значению  соответствует значение . Заметим, что  при любых n. Следовательно, .

Тогда

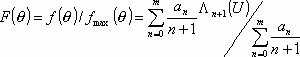
Эта формула описывает нормированную диаграмму направленности параболоидной зеркальной антенны и является расчетной. Постоянные коэффициенты  зависят от распределения поля в раскрыве зеркала. Их значения определяются системой уравнений

Рекомендуем скачать другие рефераты по теме: решебник 5 класс, реферат по социологии.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата