Предыдущая страница реферата | 1  2  3



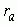– коэффициент ассоциации,

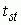– t-критерий Стьюдента,

для принятого уровня значимости (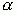) и числа степеней свободы .

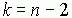Так как коэффициент ассоциации имеет прямое отношение к пирсоновскому критерию 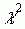, на котором он основан, то распределение вероятных значений критерия 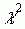является непрерывным. Качественные же признаки дискретны, их числовое значение не распределяются непрерывно. Учитывая эту особенность, в формулу (1.1) принято вносить поправку Йейтса на непрерывность вариации, равную половине объёма выборки. И формула (1.1) принимает следующий вид:

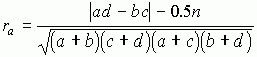. (1.3)

9. Валидность

Кратко рассмотрим природу валидности, второй из основных характеристик эффективных тестов. Тест называется валидным, если он измеряет то, для измерения чего он предназначен. Однако такое определение не разъясняет удовлетворительно значения валидности. В этом случае возникает новый вопрос: как мы узнаем, что тест измеряет то, для чего он предназначен? В действительности, существует много различных способов доказательства валидности тестов, и каждый из них соответствует разным аспектам этого значения.

Говорят, что тест является, очевидно валидным, если о нем складывается впечатление, что он измеряет именно то, что подразумевается, особенно с точки зрения испытуемых

Конкурентная валидность – эта валидность оценивается по корреляции результатов данного теста с результатами других тестов. Так, если мы пытаемся установить конкурентную валидность некоторого теста интеллекта, мы будем изучать его корреляцию с другими тестами, валидность которых установлена.

Содержательная валидность. Этот термин применяется, в основном, по отношению к тестам достижений и может быть просто объяснён следующим образом. Если можно показать, что задания теста отражают все аспекты исследуемой области поведения, то тест является, по существу, валидным, при условии, что инструкции изложены ясно. Содержательная валидность не сводится к простой очевидной валидности, которая связан с внешним видом заданий теста. Если в тесте математических навыков мы хотим протестировать умение перемножать выражения скобках и имеем задания вида 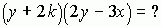, то трудно оспаривать валидность этого задания. Очевидно, содержательная валидность полезна только для тех тестов, для которых, как в данном случае, смысл, измеряемого параметра полностью ясен.

Были описаны разнообразные способы установления валидности тестов, некоторые из них коренным образом отличаются друг от друга. Из обсуждения должно быть также понятно, что не может быть какого-либо единственного показателя, демонстрирующего валидность теста. Для полной ее проверки следует учитывать множеств получаемых показателей. Более того, как это станет ясно из дальнейшего изложения, валидность теста может фактически гарантироваться логически обоснованными методами конструирования тестов.

10. Дискриминативность

Дискриминативность – это способность отдельных заданий теста и теста в целом дифференцировать обследуемых относительно “максимального” и “минимального” результата теста.

Еще одной особенностью эффективных тестов является дискриминативность. Действительно, достижение удовлетворительного распределения показателей является одной из целей разработчика теста. При помощи тщательного конструирования теста можно обеспечить соответствующий уровень дискриминативности, а это именно то, в чем тесты значительно выигрывают по сравнению с другими формами испытаний. В общем, было обнаружено, что в оценке может быть использовано около девяти градаций [1], а в опросах, вероятно, наиболее эффективно использовать три градации: ниже среднего, средний уровень и выше среднего. Дискриминативность измеряется показателем дельта Фергюсона и принимает максимальное значение при равномерном (прямоугольном) распределении показателей ().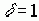

10.1 Метод Фергюсона для вычисления дискриминативности теста

Коэффициент Фергюсона – это отношение между показателем дискриминативности, полученным для некоторого теста и максимальным значением дискриминативности, которое может обеспечить такой тест.

,

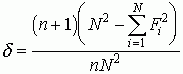где

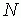– количество испытуемых,

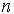– количество заданий теста,

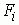– частота встречаемости каждого показателя.

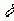= 0, когда все испытуемые получили одинаковые показатели, то есть когда нет дискриминативности. 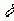= 1 при равномерном распределении заданий, в которых наиболее полно были реализованы все возможные проявления измеряемого свойства.
Скачали данный реферат: Roman, Kostjuk, Пащенко, Сарнычев, Ohrema, Irinarh.
Последние просмотренные рефераты на тему: реферат по обж, закон реферат, бесплатные шпаргалки по праву, растения реферат.

Предыдущая страница реферата | 1  2  3