
Математичнi моделi iнфляцii /Укр./
| Категория реферата: Топики по английскому языку
| Теги реферата: реферат религия, пушкин реферат
| Добавил(а) на сайт: Vasilij.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 | Следующая страница реферата
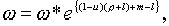 |
(2.1.7) |
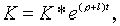 |
(2.1.8) |
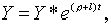 |
(2.1.9) |
де
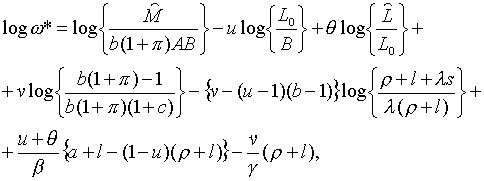 |
(2.1.10) |
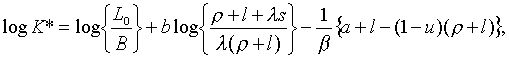 |
(2.1.11) |
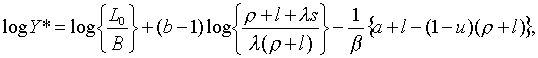 |
(2.1.12) |
Із (1.4), (2.1.8), (2.1.9) та (2.1.12) випливає,що рівноважна траекторія росту зайнятості визначається рівнянням
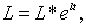 |
(2.1.13) |
де
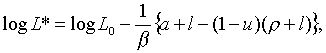
Таким чином, ця траекторія не пов’язана з оптимальною. Дійсно, порівняння (1.28) з (2.1.13) показує, що рівноважна траекторія росту зайнятості співпадає з траекторією, що відповідає постійній пропозиції грошей. Це неприйнятний наслідок політики, що описується рівнянням (2.1.1). Розглянемо тепер вплив цієї політики на стійкість системи.
З рівнянь (2.1.4) — (2.1.6) та (2.1.10) — (2.1.13) маємо
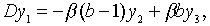 |
(2.1.14) |
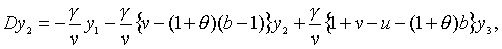 |
(2.1.15) |
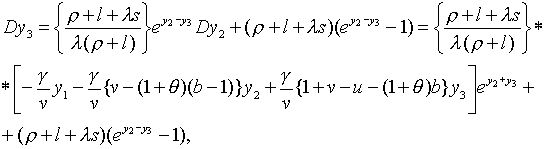 |
(2.1.16) |
де
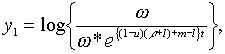
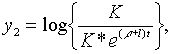
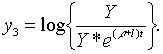
Точні траекторії зміни змінних 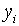 визначаються початковими значеннями цих змінних і системою рівнянь (2.1.4) — (2.1.6) та (2.1.10) — (2.1.13), а наближені траекторії – тими ж початковими значеннями і системою лінійних рівнянь, які включають (2.1.14), (2.1.15) та
визначаються початковими значеннями цих змінних і системою рівнянь (2.1.4) — (2.1.6) та (2.1.10) — (2.1.13), а наближені траекторії – тими ж початковими значеннями і системою лінійних рівнянь, які включають (2.1.14), (2.1.15) та
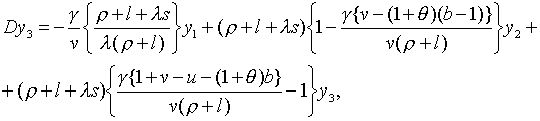 |
(2.1.17) |
Характеристичними коренями матриці коефіцієнтів останньої системи є корені рівняння
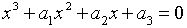 , , |
(2.1.18) |
де
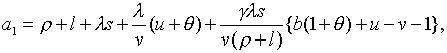
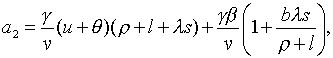
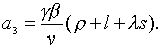
Зауважимо, що 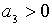 ,
, 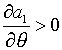 , і при умові, що
, і при умові, що 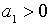 частинна похідна
частинна похідна 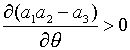 . Отже, хоч політика задана рівнянням (2.1.1) не впливає на рівноважну траекторію зайнятості (на відміну від політики, що передбачає постійну пропозицію грошей), вона може справляти стабілізуючу дію.
. Отже, хоч політика задана рівнянням (2.1.1) не впливає на рівноважну траекторію зайнятості (на відміну від політики, що передбачає постійну пропозицію грошей), вона може справляти стабілізуючу дію.
Припустимо, наприклад, що 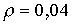 ;
; 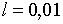 ;
; 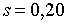 ;
; 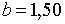 ;
; 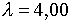 ;
; 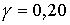 ;
; 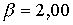 ;
; 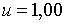 ;
; 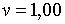 .При цих умовах і при
.При цих умовах і при 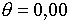 корені рівняння (2.1.18) рівні
корені рівняння (2.1.18) рівні 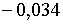 ;
; 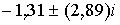 , а при
, а при 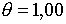 ці корені рівні
ці корені рівні 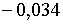 ;
; 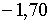 ;
; 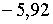 . Тобто у даному випадку вплив грошової політики приводить до поступової ліквідації ціклу і більш швидкої збіжності до довгострокового тренду.
. Тобто у даному випадку вплив грошової політики приводить до поступової ліквідації ціклу і більш швидкої збіжності до довгострокового тренду.
Розглянемо тепер політику, яка визначається рівнянням
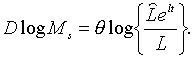 |
(2.1.19) |
З цього рівняння випливає, що при оптимальному рівні зайнятості пропозиція грошей постійна. В протилежному випадку пропорційний темп росту пропозиції грошей, є зростаючою функцією пропорціонального перевищення 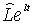 над
над 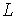 . Тепер модель описується рівняннями (1.1), (1.9) та (2.1.19).
. Тепер модель описується рівняннями (1.1), (1.9) та (2.1.19).
З (1.7), (1.8) та (1.12) маємо
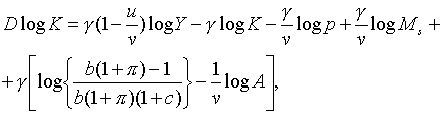 |
(2.1.20) |
що у сукупності з (1.4) та (1.5) дає
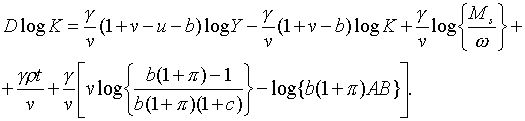 (2.1.21) (2.1.21) |
Далі, з (1.4) та (1.19) маємо
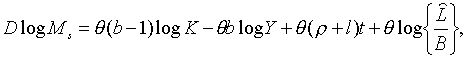 |
(2.1.22) |
що разом з (2.1.5) дає
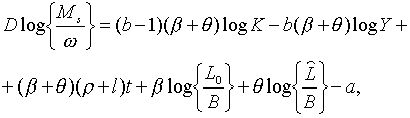 |
Категории:Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
 Главная
Главная