Claw.ru | Топики по английскому языку | On a decomposition of an element of a free metabelian group as a productof primitive elements On a decomposition of an element of a free metabelian group as a productof primitive elements | Категория реферата: Топики по английскому языку | Теги реферата: виды шпор, організація реферат | Добавил(а) на сайт: Lomonosov. Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

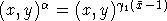
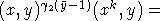
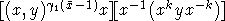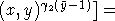
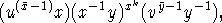
The last commutator in (3) can be added to first one in (2). We get [y-1 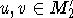, that is a product of three primitive elements.

4. A decomposition of an element of a free metabelian group of rank 2 as a product of primitive elements

For further reasonings we need the following fact: any primiti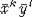ve element of a group A2 is induced by a primitive element 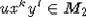, 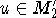. It can be explained in such way. One can go from the basis of the group M2.

The similar assertions are valid for any rank .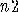

Предложение 3. Any element of group M2 can be presented as a product of not more then four primitive elements.

Доказательство. At first consider the elements in form 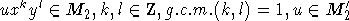. An element 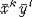is primitive in A2 by lemma 1, consequently there is a primitive element of type 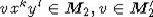. Hence, 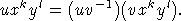Since, an element 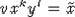is primitive, it can be included into some basis 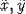inducing the same basis 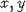of A2. After rewriting in this new basis we have:

,

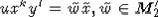and so as before

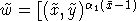
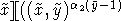
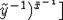
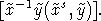
Obviously, two first elements above are primitive. Denote them as p1, p2. Finally, we have

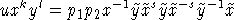
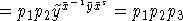, a product of three primitive elements.

If 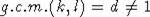, then by proposition 1 we can find an expansion 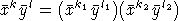as a product of two primitive elements, which correspond to primitive elements of M2: v1xk1yl1,v2xk2yl2,v1,v2 .

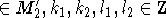Further we have the expansion

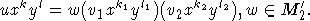
The element w(v1xk1yl1) can be presented as a product of not more then three primitive elements. We have a product of not more then four primitive elements in the general case.

5. A decomposition of elements of a free metabelian group of rank 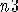as a product of primitive elements

of rank .

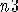
Предложение 4. Any element 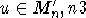can be presented as a product of not more then four primitive elements.

Доказательсво. It is well-known [2], that M'n as a module is generated by all commutators 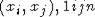. Therefore, for any 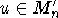there exists a presentation

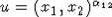
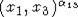
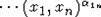
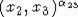
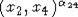
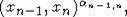
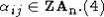
Separate the commutators from (4) into three groups in the next way.

1) 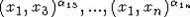- the commutators not including the element x2 but including x1.

2)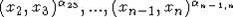 - the other commutators not including the x1.

3) And the third set consists of the commutator .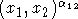

Consider an automorphism of Mn, defining by the following map:

Рекомендуем скачать другие рефераты по теме: информационные системы реферат, курсовая работа по менеджменту, тезис.

Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата